题目内容

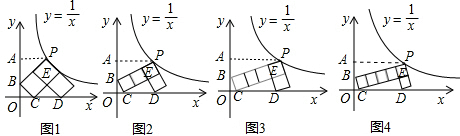
如图1～4所示，每个图中的“7”字形是由若干个边长相等的正方形拼接而成，“7”字形的一个顶点P落在反比例函数y=
1
x
的图象上，另“7”字形有两个顶点落在x轴上，一个顶点落在y轴上．
（1）图1中的每一个小正方形的面积是______；
（2）按照图1→图2→图→图4→…这样的规律拼接下去，第n个图形中每一个小正方形的面积是______．（用含n的代数式表示）
（1）作PA⊥y轴于A，图中的“7”字形与坐标轴的交点分别为B、C、D，如图1，
设每一个小正方形的边长为a，
易证得Rt△ECD∽Rt△OBC∽Rt△APB，
∴
CE
OB
=
DE
OC
，
CE
AP
=
DE
AB
，
∴
OB
OC
=
AP
AB
=
CE
ED
=
a
a
=1，
在RtOBC中，BC=a，
∵OB2+OC2=BC2=a2，OB=OC，
∴OB=
a
2
，
在Rt△ABP中，PB=2a，
∵AB2+AP2=BP2=4a2，AB=AP，
∴AB=AP=
2
2
a，
∴OA=
3a
2
，
∴P点坐标为（
2a
2
，
3a
2
），
∴
2a
2
•
3a
2
=1，
∴a2=
1
3
；

（2）如图2，同样得到Rt△ECD∽Rt△OBC∽Rt△APB，
∴
CE
OB
=
DE
OC
，
CE
AP
=
DE
AB
，
∴
OB
OC
=
AP
AB
=
CE
ED
=
2a
a
=2，
在RtOBC中，BC=a，
∵OB2+OC2=BC2=a2，OB=2OC，
∴OB=
2a
5
，
在Rt△ABP中，PB=3a，
∵AB2+AP2=BP2=9a2，AB=2AP，
∴AB=
3a
5
，AP=
6a
5

∴OA=
5a
5
，
∴P点坐标为（
6a
5
，
5a
5
），
∴
6a
5
•
5a
5
=1，
∴a2=
5
30
；
如图3，易证得Rt△ECD∽Rt△OBC∽Rt△APB，
∴
CE
OB
=
DE
OC
，
CE
AP
=
DE
AB
，
∴
OB
OC
=
AP
AB
=
CE
ED
=
3a
a
=3，
同理可得a2=
10
84
；
如图4，易证得Rt△ECD∽Rt△OBC∽Rt△APB，
∴
CE
OB
=
DE
OC
，
CE
AP
=
DE
AB
，
∴
OB
OC
=
AP
AB
=
CE
ED
=
4a
a
=4，
同理可得a2=
17
180
；
∵第1个图每一个小正方形的面积=
1
3
=
2
2×3
=
12+1
1×(1+1)×(2+1)
；
第2个图每一个小正方形的面积=
5
30
=
5
6×5
=
22+1
2×(2+1)×(2×2+1)
；
第3个图每一个小正方形的面积=
10
12×7
=
32+1
3×(3+1)(2×3+1)
；
第4个图每一个小正方形的面积=
17
180
=
17
4×5×9
=
42+1
4×(4+1)(2×4+1)
，
∴第n个图每一个小正方形的面积=
n2+1
n(n+1)(2n+1)
．
故答案为（1）
1
3
；（2）
n2+1
n(n+1)(2n+1)
．
练习册系列答案
相关题目
如图，反比例函数y=
k
x
的图象经过点A（2，m），过点A作AB垂直y轴于点B，△AOB的面积为5．
（1）求k和m的值；
（2）已知点C（-5，-2）在反比例函数图象上，直线AC交x轴于点M，求△AOM的面积；
（3）过点C作CD⊥x轴于点D，连接BD，试证明四边形ABDC是梯形．
如图，直线AC与双曲线y=
k
x
在第四象限交于点A（x0，y0），交x轴于点C，且AO=
13
，点A的横坐标为2，过点A作AB⊥x轴于点B，且S△ABC：S△ABO=4：1．
（1）求k的值及直线AC的解析式；
（2）在第四象限内，双曲线y=
k
x
上有一动点D（m，n），设△BCD的面积为S，求S与m的函数关系式．
如图，点P在反比例函数y=
1
x
（x＞0）的图象上，且横坐标为2．若将点P先向右平移两个单位，再向上平移一个单位后所得图象为点P′．则经过点P'的反比例函数图象的解析式是______．
如图，在平面直角坐标系xOy中，已知矩形AOBC，AO=2，BO=3，函数y=
k
x
的图象经过点C．
（1）直接写出点C的坐标；
（2）将矩形AOBC分别沿直线AC，BC翻折，所得到的矩形分别与函数y=
k
x
（x＞0）交于点E，F求线段EF．
（3）若点P、Q分别在函数y=
k
x
图象的两个分支上，请直接写出线段P、Q两点的最短距离（不需证明）；并利用图象，求当
k
x
≤x时x的取值范围．
如图，双曲线y=
k
x
过点A（-1，3）．
（1）求k的值；
（2）若过点A的直线y=-2x+b与x轴交于点B，求△AOB的面积．
如图，直线y=kx+4与函数y=
m
x
（x＞0，m＞0）的图象交于A、B两点，且与x、y轴分别交于C、D两点．
（1）若△COD的面积是△AOB的面积的
2
倍，求k与m之间的函数关系式；
（2）在（1）的条件下，是否存在k和m，使得以AB为直径的圆经过点P（2，0）？若存在，求出k和m的值；若不存在，请说明理由．
●探究：
（1）在图中，已知线段AB，CD，其中点分别为E，F．
①若A（-1，0），B（3，0），则E点坐标为______；
②若C（-2，2），D（-2，-1），则F点坐标为______；
（2）在图中，已知线段AB的端点坐标为A（a，b），B（c，d），求出图中AB中点D的坐标（用含a，b，c，d的代数式表示），并给出求解过程．
●归纳：
无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（a，b），B（c，d），AB中点为D（x，y）时，x=______，y=______．（不必证明）
●运用：
在图中，一次函数y=x-2与反比例函数y=
3
x
的图象交点为A，B．
①求出交点A，B的坐标；
②若以A，O，B，P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标．
如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=
k
x
的图象上．若点A的坐标为（-2，-2），则k的值为（　　）
A．-2B．4C．3D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网