题目内容
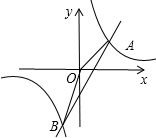
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
的图象上.若点A的坐标为(-2,-2),则k的值为( )

| k |
| x |
| A.-2 | B.4 | C.3 | D.2 |

可以设点C的坐标是(m,n),
设AB与x轴交于点M,则△BMO∽△BAD,
则
=
,
因为AD=2+m,AB=2+n,OM=2,BM=n,
因而得到
=
,
即mn=4,
点(m,n)在反比例函数y=
的图象上,
代入得到:k=xy=mn=4,
故选B.
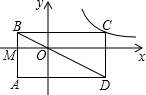
设AB与x轴交于点M,则△BMO∽△BAD,
则
| BM |
| AB |
| OM |
| AD |
因为AD=2+m,AB=2+n,OM=2,BM=n,
因而得到
| n |
| 2+n |
| 2 |
| 2+m |
即mn=4,
点(m,n)在反比例函数y=
| k |
| x |
代入得到:k=xy=mn=4,
故选B.


练习册系列答案
相关题目





 不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.
不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.