题目内容
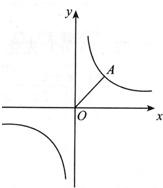
如图,在平面直角坐标系xOy中,已知矩形AOBC,AO=2,BO=3,函数y=
的图象经过点C.
(1)直接写出点C的坐标;
(2)将矩形AOBC分别沿直线AC,BC翻折,所得到的矩形分别与函数y=
(x>0)交于点E,F求线段EF.
(3)若点P、Q分别在函数y=
图象的两个分支上,请直接写出线段P、Q两点的最短距离(不需证明);并利用图象,求当
≤x时x的取值范围.

| k |
| x |
(1)直接写出点C的坐标;
(2)将矩形AOBC分别沿直线AC,BC翻折,所得到的矩形分别与函数y=
| k |
| x |
(3)若点P、Q分别在函数y=
| k |
| x |
| k |
| x |

(1)∵四边形AOBC是矩形,OA=2,OC=3
∵C(3,2);
(2)∵点C(3,2)在反比例函数y=
的图象上,
∴2=
,即k=6,
∴此反比例函数的解析式为y=
,
∵AD=OA=2,BG=OC=3,
∴D(0,4),G(6,0),
当y=4时,4=
,解得x=
,
∴E(
,4)
把x=6代入y=
得y=1,
∴F(6,1),
∴EF=
=
;
(3)当P与Q的横纵坐标绝对值相等时,PQ的距离最小,
∴将y=x代入y=
得x2=6,
解得:x=±
,
∴P(
,
),Q(-
,-
),
∴此时PQ的距离最短,最短距离PQ=
=4
,即PQ最小值为4
.
∵由x=
时,x1=
,x2=-
,
∵根据图象,当x≥
时,y随着x的增大而减小;
当-
≤x<0时,y随着x的增大而小.
∴当
≤x时,x的取值范围为:x≥
或-
≤x<0.
∵C(3,2);
(2)∵点C(3,2)在反比例函数y=
| k |
| x |
∴2=
| k |
| 3 |
∴此反比例函数的解析式为y=
| 6 |
| x |
∵AD=OA=2,BG=OC=3,
∴D(0,4),G(6,0),
当y=4时,4=
| 6 |
| x |
| 3 |
| 2 |
∴E(
| 3 |
| 2 |
把x=6代入y=
| 6 |
| x |
∴F(6,1),
∴EF=
(
|
3
| ||
| 2 |
(3)当P与Q的横纵坐标绝对值相等时,PQ的距离最小,
∴将y=x代入y=
| 6 |
| x |
解得:x=±
| 6 |
∴P(
| 6 |
| 6 |
| 6 |
| 6 |
∴此时PQ的距离最短,最短距离PQ=
(2
|
| 3 |
| 3 |
∵由x=
| 6 |
| x |
| 6 |
| 6 |
∵根据图象,当x≥
| 6 |
当-
| 6 |
∴当
| 6 |
| x |
| 6 |
| 6 |

练习册系列答案
相关题目




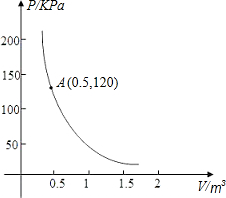 不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.
不变时,气球内气体的气压P(KPa)是气体体积V(m3)的反比例函数,其图象如图所示.