题目内容
【题目】在平面直角坐标系中，抛物线y=
x2﹣bx+c与x轴交于点A（8，0）、B（2，0）两点，与y轴交于点C．
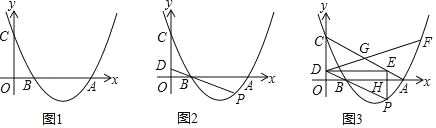
（1）如图1，求抛物线的解析式；
（2）如图2，点P为第四象限抛物线上一点，连接PB并延长交y轴于点D，若点P的横坐标为t，CD长为d，求d与t的函数关系式（并求出自变量t的取值范围）；
（3）如图3，在（2）的条件下，连接AC，过点P作PH⊥x轴，垂足为点H，延长PH交AC于点E，连接DE，射线DP关于DE对称的射线DG交AC于点G，延长DG交抛物线于点F，当点G为AC中点时，求点F的坐标．
【答案】见解析．
【解析】
试题分析：（1）利用待定系数法直接求出抛物线解析式；
（2）先表示出BH，PH，进而得出∠HBP的正切值，再用等角的同名三角函数即可表示出OD，即可得出结论；
（3）先求出直线AC解析式，进而判断出四边形DOMN是矩形，最后用三角函数和对称性求出t，即可得出OD和tan∠GDN=
，即可得出结论．
试题解析：证明：（1）∵抛物线y=
x2-bx+c过A（8，0）、B（2，0）两点，
∴
，
∴
，
∴抛物线的解析式为：y=
x2﹣
x+4
（2）如图2，
过点P作PH⊥AB于点H，
设点P（t，
t2-
t+4）
∴BH=t﹣2，PH=-
t2-
t+4
∴tan∠HBP=
=
，
∵∠OBD=∠HBP，
∴tan∠OBD=tan∠HBP，
∴-
=
，
∴OD=-
t+4，
∴CD=4﹣OD=
∴d=
t（2＜t＜8），
（3）如图3，
设直线 AC的解析式为y=kx+b，
∴
∴
，
∴直线AC的解析式为y=-
x+4，
∴点E（t，-
t+4）
∴EH=OD=-
t+4，
∵EH∥OD，
∴四边形DOHE是矩形，
∴DE∥OH，
取AO的中点M，
连接GM，交DE于点N，
∴GM∥OC，
∴GN⊥DE，
∴四边形DOMN是矩形，
∴OD=NM=-
t+4，NG=2﹣MN=
t-2，
∵DN=OM=4
tan∠GDN=
=
t-
，
∵由对称性得∠PDE=∠GDE=∠HBP
tan∠GDN=tan∠HBP，
∴
t-
=-
(t-8)，
∴t=
∴OD=
，
∴tan∠GDN=
，
设点F（m，
m0-
m+4
过点F作FK⊥DE交延长线于点K，
tan∠GDN=
=
=
，
∴m1=10,m2=
（舍），
∴F（10，4），
