ЬтФПФкШн
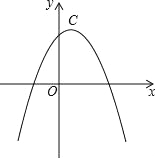
ЁОЬтФПЁПЃЈБОЬтТњЗж12ЗжЃЉШчЭМЃЌвджБНЧШ§НЧаЮAOCЕФжБНЧЖЅЕуOЮЊдЕуЃЌвдOCЁЂOAЫљдкжБЯпЮЊxжсКЭyжсНЈСЂЦНУцжБНЧзјБъЯЕЃЌЕуAЃЈ0ЃЌ aЃЉЃЌCЃЈbЃЌ0ЃЉТњзу![]() ЁЃ
ЁЃ
ЃЈ1ЃЉдђCЕуЕФзјБъЮЊ__________;AЕуЕФзјБъЮЊ__________ЃЎ
ЃЈ2ЃЉвбжЊзјБъжсЩЯгаСНЖЏЕуPЁЂQЭЌЪБГіЗЂЃЌPЕуДгCЕуГіЗЂбиxжсИКЗНЯђвд1ИіЕЅЮЛГЄЖШУПУыЕФЫйЖШдШЫйвЦЖЏЃЌQЕуДгOЕуГіЗЂвд2ИіЕЅЮЛГЄЖШУПУыЕФЫйЖШбиyжсе§ЗНЯђвЦЖЏЃЌЕуQЕНДяAЕуећИідЫЖЏЫцжЎНсЪјЃЎACЕФжаЕуDЕФзјБъЪЧЃЈ1,2ЃЉЃЌЩшдЫЖЏЪБМфЮЊtЃЈtЃО0ЃЉУыЃЎЮЪЃКЪЧЗёДцдкетбљЕФtЃЌЪЙ![]() ,ШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
,ШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
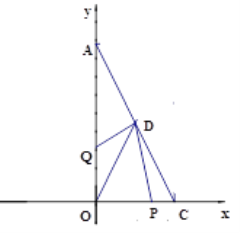
ЃЈ3ЃЉЕуFЪЧЯпЖЮACЩЯвЛЕуЃЌТњзуЁЯFOC=ЁЯFCO, ЕуGЪЧЕкЖўЯѓЯожавЛЕуЃЌСЌOG,ЪЙЕУЁЯAOG=ЁЯAOFЃЎЕуEЪЧЯпЖЮOAЩЯвЛЖЏЕуЃЌСЌCEНЛOFгкЕуHЃЌ ЕБЕуEдкЯпЖЮOAЩЯдЫЖЏЕФЙ§ГЬжаЃЌ![]() ЕФжЕЪЧЗёЛсЗЂЩњБфЛЏ,ШєВЛБфЃЌЧыЧѓГіЫќЕФжЕЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЪЧЗёЛсЗЂЩњБфЛЏ,ШєВЛБфЃЌЧыЧѓГіЫќЕФжЕЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
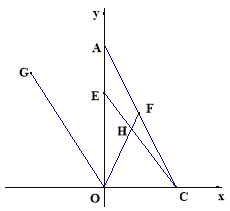
ЁОД№АИЁПЃЈ1ЃЉAЃЈ0,4ЃЉ CЃЈ2,0ЃЉЃЛЃЈ2ЃЉДцдкЃЌt=1ЃЛЃЈ3ЃЉВЛБфЃЌжЕЮЊ2ЃЎ
ЁОНтЮіЁП
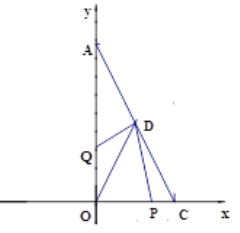
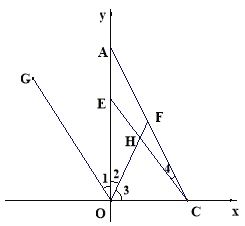
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЖўДЮИљЪНКЭОјЖджЕЕФЗЧИКадЧѓГіa,bжЕЃЌНјЖјжЊЕРA,CЕФзјБъЃЛЃЈ2ЃЉгЩЬѕМўжЊ:ЕуQЕНДяAЕуећИідЫЖЏЫцжЎНсЪј,QЕуДгOЕудЫЖЏЕНAЕуЪБМфЮЊ2Уы, Ёр 0ЃМtЁм2ЃЌЕуQдкЯпЖЮAOЩЯ,PдкЯпЖЮOCЩЯЃЌЁпCP=t ЃЌOC=2ЃЌ ЁрOP=2-t,OQ=2t,ЁпDЕФзјБъЪЧЃЈ1,2ЃЉЃЌМйЩшДцдкЃЌСаГіЁїODPКЭЁїODQУцЛ§ЯрЕШЕФЪНзгЃЌПДЗћКЯЬѕМўЕФtжЕЪЧЗёДцдкЃЛЃЈ3ЃЉИљОнвбжЊЬѕМўЯШжЄУїOGЁЮAC,ШЛКѓЙ§HЕузіACЕФЦНааЯпНЛOAгкM,НЛOCгкNЃЌРћгУСНжБЯпЦНааФкДэНЧЯрЕШЃЌКЭШ§НЧаЮЭтНЧаджЪЃЌЩшЗЈНЋЁЯOHCзЊЛЏГЩЁЯ1ЃЋЁЯ2ЃЋЁЯ4ЃЌНЋЁЯOECзЊЛЏГЩЁЯ1ЃЋЁЯ4ЃЌетбљОЭЧѓГіСЫЫљЧѓЮЪЬтЕФБШжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЖўДЮИљЪНКЭОјЖджЕЕФЗЧИКадЕУЃЌb-2=0,Ёрb=2,a-2b=0,МДa-4=0,Ёрa=4ЃЌЁрAЃЈ0,4ЃЉ CЃЈ2,0ЃЉЃЛЃЈ2ЃЉгЩЬѕМўжЊЃКPЕуДгCЕудЫЖЏЕНOЕуЪБМфЮЊ2УыЃЌQЕуДгOЕудЫЖЏЕНAЕуЪБМфЮЊ2Уы,ЕуQЕНДяAЕуећИідЫЖЏЫцжЎНсЪјЃЌЁр0<tЁм2ЃЌДЫЪБЕуQдкЯпЖЮAOЩЯ,PдкЯпЖЮOCЩЯЃЌМДCP=t ,OP=2-t,OQ=2t,ЁпDЕФзјБъЪЧЃЈ1,2ЃЉЃЌЁр ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁр2-t=tЃЌЁрt=1,ЗћКЯЬѕМўЃЌЁрДцдкетбљЕФtЃЌЪЙ
ЃЌЁр2-t=tЃЌЁрt=1,ЗћКЯЬѕМўЃЌЁрДцдкетбљЕФtЃЌЪЙ![]() ,ДЫЪБt=1ЃЎ
,ДЫЪБt=1ЃЎ
ЯШИљОнвбжЊЬѕМўжЄУїOGЁЮAC ЃЌШчЭМЃКЁпЁЯ2ЃЋЁЯ3=90 ЃЌЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯFCOЁрЁЯ1ЃЋЁЯ2ЃЋЁЯ3ЃЋЁЯFCO=2ЃЈЁЯ2ЃЋЁЯ3ЃЉ=180,ЁрOGЁЮAC ,Й§HЕузїACЕФЦНааЯпНЛOAгкM,НЛOCгкNЃЌдђOGЁЮMNЁЮAC,ЁрЁЯGOF=ЁЯ1ЃЋЁЯ2=ЁЯOHN,ЁЯNHC=ЁЯ4ЃЌРћгУШ§НЧаЮЭтНЧаджЪПЩЕУЃКЁЯOEC=ЁЯOACЃЋЁЯ4=ЁЯ1ЃЋЁЯ4ЃЌЁрЁЯOHC=ЁЯOHNЃЋЁЯNHC=ЁЯ1ЃЋЁЯ2ЃЋЁЯ4,Ёр![]() ,Ёр
,Ёр![]() ЕФжЕВЛБфЃЎЦфжЕЮЊ2ЃЎ
ЕФжЕВЛБфЃЎЦфжЕЮЊ2ЃЎ

 ХргХШ§КУЩњЯЕСаД№АИ
ХргХШ§КУЩњЯЕСаД№АИ гХЛЏзївЕЩЯКЃПЦММЮФЯзГіАцЩчЯЕСаД№АИ
гХЛЏзївЕЩЯКЃПЦММЮФЯзГіАцЩчЯЕСаД№АИ