题目内容
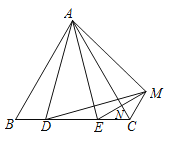
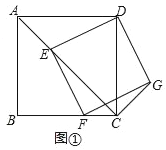
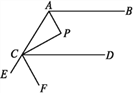
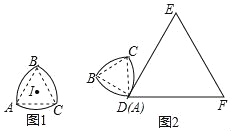
【题目】如图1，等边△ABC的边长为3，分别以顶点B、A、C为圆心，BA长为半径作弧AC、弧CB、弧BA，我们把这三条弧所组成的图形称作莱洛三角形，显然莱洛三角形仍然是轴对称图形．设点I为对称轴的交点，如图2，将这个图形的顶点A与等边△DEF的顶点D重合，且AB⊥DE，DE=2π，将它沿等边△DEF的边作无滑动的滚动，当它第一次回到起始位置时，这个图形在运动中扫过区域面积是（ ）
A. 18π B. 27π C. 
π D. 45π
【答案】B
【解析】
先判断出莱洛三角形等边△DEF绕一周扫过的面积如图所示，利用矩形的面积和扇形的面积之和即可.
如图1中，
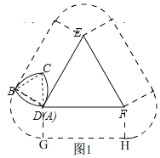
∵等边△DEF的边长为2π，等边△ABC的边长为3，
∴S矩形AGHF=2π×3=6π，
由题意知，AB⊥DE，AG⊥AF，
∴∠BAG=120°，
∴S扇形BAG=
=3π，
∴图形在运动过程中所扫过的区域的面积为3（S矩形AGHF+S扇形BAG）=3（6π+3π）=27π；
故选：B．
学而优衔接教材南京大学出版社系列答案
【题目】某甜品店用
，
两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
份，乙款甜品
份，共用去原料2000克．
原料 款式 |
（克） |
（克） |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
（1）求关于的函数表达式；
（2）已知每份甲甜品的利润为5元，每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元，则至少要用去原料多少克？
【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具，共80个． 制作的道具需要甲、乙两种材料组合而成，现有甲种材料700件，乙种材料500件，已知组装A、B两种道具所需的甲、乙两种材料，如下表所示：
甲种材料（件） | 乙种材料（件） | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算，制作一个A道具的费用为5元，一个B道具的费用为4.5元． 设组装A种道具x个，所需总费用为y元．
（1）求y与x的函数关系式，并求出x的取值范围；
（2）问组装A种道具多少个时，所需总费用最少，最少费用是多少？
