题目内容
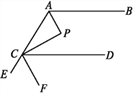
【题目】如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
【答案】(1)∠CAP=90°-α; (2)证明见解析;(3)证明见解析;
【解析】试题分析:(1)由角平分线的定义可得∠PAC=α,在Rt△PAC中根据直角三角形的性质可求得∠ACP;
(2)结合(1)可求得∠ACD,可证明∠ACD+∠BAC=180°,可证明AB∥CD;
(3)由平行线的性质可得∠ECF=∠CAP,∠ECD=∠CAB,结合条件可证得∠ECF=∠FCD,可证得结论.
试题解析:(1)解:∵AP平分∠BAC,∴∠CAP=∠BAP=α.
∵∠P=90°,∴∠ACP=90°-∠CAP=90°-α;
(2)证明:由(1)可知∠ACP=90°-α.
∵CP平分∠ACD,∴∠ACD=2∠ACP=180°-2α.
又∠BAC=2∠BAP=2α,∴∠ACD+∠BAC=180°,∴AB∥CD;
(3)证明:∵AP∥CF,∴∠ECF=∠CAP=α.
由(2)可知AB∥CD,∴∠ECD=∠CAB=2α,∴∠DCF=∠ECD-∠ECF=α,∴∠ECF=∠DCF,∴CF平分∠DCE.

练习册系列答案
相关题目
