题目内容
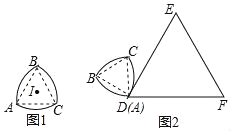
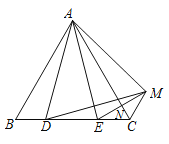
【题目】如图,在等边![]() 中,
中,![]() ,将线段
,将线段![]() 沿
沿![]() 翻折,得到线段
翻折,得到线段![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() 以下说法:①
以下说法:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】D
【解析】
由△ABD≌△ACE,△ACE≌△ACM,△ABC是等边三角形可以对①②进行判断,由AC垂直平分EM和直角三角形的性质可对③进行判断,由△ADM是等边三角形可对④进行判断.
解:∵△ABC是等边三角形,
∴AB=AC,∠B=∠BAC=∠ACB=60°,
∵BD=CE,
∴△ABD≌△ACE(SAS)
∴AD=AE,∠BAD=∠CAE
∵线段![]() 沿
沿![]() 翻折,
翻折,
∴AE=AM,∠CAE=∠CAM,
∴![]() ,故①正确,
,故①正确,
∴△ACE≌△ACM(SAS)
∴∠ACE=∠ACM=60°,故②正确,
由轴对称的性质可知,AC垂直平分EM,
∴∠CNE=∠CNM=90°,
∵∠ACM =60°,
∴∠CMN=30°,
∴在Rt△CMN中,![]() ,即
,即![]() ,故③正确,
,故③正确,
∵∠BAD=∠CAE,∠CAE=∠CAM,
∴∠BAD=∠CAM,
∵∠∠BAD+∠CAD=60°,
∴∠CAM +∠CAD=60°,
即∠DAM=60°,又AD=AM
∴△ADM为等边三角形,
∴![]() 故④正确,
故④正确,
所以正确的有4个,
故答案为:D.

练习册系列答案
相关题目
【题目】中国移动某套餐推出了如下两种流量计费方式:
月租费/元 | 流量费(元/ | |
方式一 | 8 | 1 |
方式二 | 28 | 0.5 |
(1)设一个月内用移动电话使用流量为![]() ,方式一总费用
,方式一总费用![]() 元,方式二总费用
元,方式二总费用![]() 元(总费用不计通话费及其它服务费).写出
元(总费用不计通话费及其它服务费).写出![]() 和
和![]() 关于
关于![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
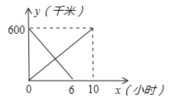
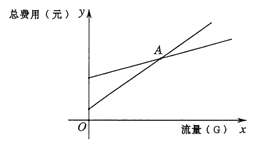
(2)如图为在同一平面直角坐标系中画出(1)中的两个函数图象的示意图,记它们的交点为点![]() ,求点
,求点![]() 的坐标,并解释点
的坐标,并解释点![]() 坐标的实际意义;
坐标的实际意义;
(3)根据(2)中函数图象,结合每月使用的流量情况,请直接写出选择哪种计费方式更合算.