题目内容
【题目】某甜品店用
，
两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
份，乙款甜品
份，共用去原料2000克．
原料 款式 |
（克） |
（克） |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
（1）求关于的函数表达式；
（2）已知每份甲甜品的利润为5元，每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元，则至少要用去原料多少克？
【答案】（1）
；（2）至少要用去
原料2200克．
【解析】
（1）根据题意得到x,y的关系式，即可求解；
（2）先根据题意列出不等式求出x的取值，再列出w的函数关系，再根据一次函数的性质即可求解．
（1）由题意：
，化简得，
（2）由题意：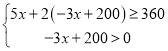
，
解不等式组得：
；
设用去原料
克，则
∵
，随
的增大而减少.
∴当
时，
克
答：至少要用去原料2200克．
作业辅导系列答案【题目】某校为了解九年级学生的视力情况，随机抽样调查了部分九年级学生的视力，以下是根据调查结果绘制的统计图表的一部分．
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 2 |
B | 4.25＜x≤4.55 | |
C | 4.55＜x≤4.85 | 20 |
D | 4.85＜x≤5.15 | |
E | 5.15＜x≤5.45 | 3 |
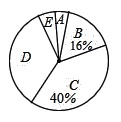
根据以上信息，解答下列问题：
（1）在被调查学生中，视力在3.95≤x≤4.25范围内的人数为 人，在4.25＜x≤4.55范围内的学生数占被调查的学生数的百分比为 %．
（2）本次调查的样本容量是 ，视力在4.85＜x≤5.15范围内的学生数占被调查学生数的百分比是 %．
（3）本次调查中，视力的中位数落在 组．
（4）若该校九年级有350名学生，估计视力超过4.85的学生数．
【题目】某工厂准备在春节前生产甲、乙两种型号的新年礼盒共 80 万套，两种礼盒的成本和售价如下表所示；
甲 | 乙 | |
成本（元/套） | 25 | 28 |
售价（元/套） | 30 | 38 |
（1）该工厂计划筹资金 2150 万元，且全部用于生产甲乙两种礼盒，则这两种礼盒各生产多少万套？
（2）经过市场调查，该厂决定在原计划的基础上增加生产甲种礼盒
万套，增加生产乙种礼盒
万套（，都为正整数），且两种礼盒售完后所获得的总利润恰为 690 万元，请问该工厂有几种生产方案？并写出所有可行的生产方案．
（3）在（2）的情况下，设实际生产的两种礼盒的总成本为
万元，请写出与的函数关系式，并求出当 为多少时成本有最小值，并求出成本的最小值为多少万元？