题目内容
【题目】已知OA,OB是⊙O的半径,且OA⊥OB,垂足为O,P是射线OA上的一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交射线OA于点E.
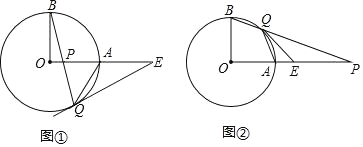
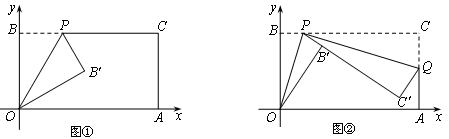
(1)如图①,点P在线段OA上,若∠OBQ=15°,求∠AQE的大小;
(2)如图②,点P在OA的延长线上,若∠OBQ=65°,求∠AQE的大小.
【答案】(1)30°;(2)20°;
【解析】
(1)利用圆切线的性质求解;
(2) 连接OQ,利用圆的切线性质及角之间的关系求解。
(1)如图①中,连接OQ.
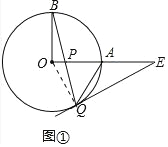
∵EQ是切线,
∴OQ⊥EQ,
∴∠OQE=90°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠AQB=![]() ∠AOB=45°,
∠AOB=45°,
∵OB=OQ,
∴∠OBQ=∠OQB=15°,
∴∠AQE=90°﹣15°﹣45°=30°.
(2)如图②中,连接OQ.
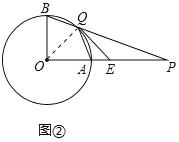
∵OB=OQ,
∴∠B=∠OQB=65°,
∴∠BOQ=50°,
∵∠AOB=90°,
∴∠AOQ=40°,
∵OQ=OA,
∴∠OQA=∠OAQ=70°,
∵EQ是切线,
∴∠OQE=90°,
∴∠AQE=90°﹣70°=20°.

【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 2 |
B | 4.25<x≤4.55 | |
C | 4.55<x≤4.85 | 20 |
D | 4.85<x≤5.15 | |
E | 5.15<x≤5.45 | 3 |
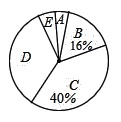
根据以上信息,解答下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人,在4.25<x≤4.55范围内的学生数占被调查的学生数的百分比为 %.
(2)本次调查的样本容量是 ,视力在4.85<x≤5.15范围内的学生数占被调查学生数的百分比是 %.
(3)本次调查中,视力的中位数落在 组.
(4)若该校九年级有350名学生,估计视力超过4.85的学生数.