题目内容
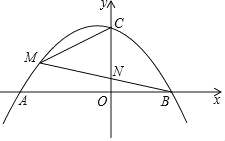
【题目】如图,抛物线y=ax2+ax﹣12a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点M是第二象限内抛物线上一点,BM交y轴于N.
(1)求点A、B的坐标;
(2)若BN=MN,且S△MBC=![]() ,求a的值;
,求a的值;
(3)若∠BMC=2∠ABM,求![]() 的值.
的值.
【答案】(1)A(﹣4,0),B(3,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)设y=0,可求x的值,即求A,B的坐标;
(2)作MD⊥x轴,由CO∥MD可得OD=3,把x=-3代入解析式可得M点坐标,可得ON的长度,根据S△BMC=![]() ,可求a的值;
,可求a的值;
(3)过M点作ME∥AB,设NO=m,![]() =k,可以用m,k表示CO,EO,MD,ME,可求M点坐标,代入可得k,m,a的关系式,由CO=2km+m=-12a,可得方程组,解得k,即可求结果.
=k,可以用m,k表示CO,EO,MD,ME,可求M点坐标,代入可得k,m,a的关系式,由CO=2km+m=-12a,可得方程组,解得k,即可求结果.
(1)设y=0,则0=ax2+ax﹣12a (a<0),
∴x1=﹣4,x2=3,
∴A(﹣4,0),B(3,0)
(2)如图1,作MD⊥x轴,

∵MD⊥x轴,OC⊥x轴,
∴MD∥OC,
∴![]() =
=![]() 且NB=MN,
且NB=MN,
∴OB=OD=3,
∴D(﹣3,0),
∴当x=﹣3时,y=﹣6a,
∴M(﹣3,﹣6a),
∴MD=﹣6a,
∵ON∥MD
∴![]() ,
,
∴ON=﹣3a,
根据题意得:C(0,﹣12a),
∵S△MBC=![]() ,
,
∴![]() (﹣12a+3a)×6=
(﹣12a+3a)×6=![]() ,
,
a=﹣![]() ,
,
(3)如图2:过M点作ME∥AB,
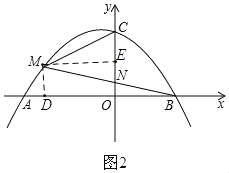
∵ME∥AB,
∴∠EMB=∠ABM且∠CMB=2∠ABM,
∴∠CME=∠NME,且ME=ME,∠CEM=∠NEM=90°,
∴△CME≌△MNE,
∴CE=EN,
设NO=m,![]() =k(k>0),
=k(k>0),
∵ME∥AB,
∴![]() =
=![]() =k,
=k,
∴ME=3k,EN=km=CE,
∴EO=km+m,
CO=CE+EN+ON=2km+m=﹣12a,
即![]() ,
,
∴M(﹣3k,km+m),
∴km+m=a(9k2﹣3k﹣12),
(k+1)×![]() =(k+1)(9k﹣12),
=(k+1)(9k﹣12),
∴![]() =9k-12,
=9k-12,
∴k=![]() ,
,
∴![]() .
.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】中国移动某套餐推出了如下两种流量计费方式:
月租费/元 | 流量费(元/ | |
方式一 | 8 | 1 |
方式二 | 28 | 0.5 |
(1)设一个月内用移动电话使用流量为![]() ,方式一总费用
,方式一总费用![]() 元,方式二总费用
元,方式二总费用![]() 元(总费用不计通话费及其它服务费).写出
元(总费用不计通话费及其它服务费).写出![]() 和
和![]() 关于
关于![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
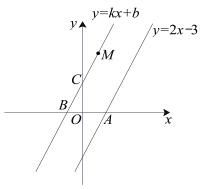
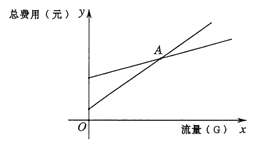
(2)如图为在同一平面直角坐标系中画出(1)中的两个函数图象的示意图,记它们的交点为点![]() ,求点
,求点![]() 的坐标,并解释点
的坐标,并解释点![]() 坐标的实际意义;
坐标的实际意义;
(3)根据(2)中函数图象,结合每月使用的流量情况,请直接写出选择哪种计费方式更合算.
【题目】某工厂准备在春节前生产甲、乙两种型号的新年礼盒共 80 万套,两种礼盒的成本和售价如下表所示;
甲 | 乙 | |
成本(元/套) | 25 | 28 |
售价(元/套) | 30 | 38 |
(1)该工厂计划筹资金 2150 万元,且全部用于生产甲乙两种礼盒,则这两种礼盒各生产多少万套?
(2)经过市场调查,该厂决定在原计划的基础上增加生产甲种礼盒![]() 万套,增加生产乙种礼盒
万套,增加生产乙种礼盒![]() 万套(
万套(![]() ,
,![]() 都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
(3)在(2)的情况下,设实际生产的两种礼盒的总成本为![]() 万元,请写出
万元,请写出![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当 ![]() 为多少时成本
为多少时成本![]() 有最小值,并求出成本
有最小值,并求出成本![]() 的最小值为多少万元?
的最小值为多少万元?