题目内容
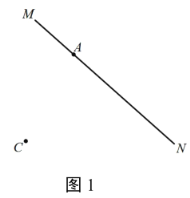
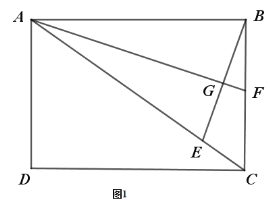
【题目】如图1, 矩形![]() 中,点
中,点![]() 在
在![]() 上,连接
上,连接![]() ,作
,作![]() 分别交
分别交![]() 于
于![]() 于
于![]() .
.
(1)若![]() 求
求![]() 的长;
的长;
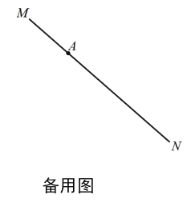
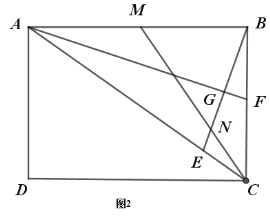
(2)如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,若
,若![]()
②求证: ![]()
②求证: ![]()
【答案】(1)![]() ;(2)①见解析;②见解析
;(2)①见解析;②见解析
【解析】
(1)根据勾股定理得出AC和EC的长度,由垂直平分线可得EF=BF,最后根据勾股定理即可求出FC的长度.
(2)①过![]() 作
作![]() ,交
,交![]() 于
于![]() ,求证
,求证![]() 即可得到MN=2CN.
即可得到MN=2CN.
②延长![]() 交
交![]() 于
于![]() ,易证
,易证![]() 得BM=2CP,进而证明
得BM=2CP,进而证明![]() 得到
得到![]() ,最后就可证明出
,最后就可证明出![]()
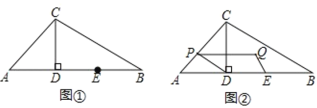
解:![]() 如图,连接
如图,连接![]() ,
,
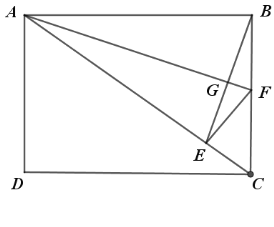
∵AB=AE=4,BC=3,
∴![]() ,EC=AC-AE=1
,EC=AC-AE=1
![]() ,
,
∴BG=GE,即AF为![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]()
![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() ①过
①过![]() 作
作![]() ,交
,交![]() 于
于![]() ,
,
![]() 为
为![]() 中点,
中点,![]()
∴MH是△ABE的中位线
∴BE=2MH
![]() ,
,
![]() ,
,
![]()
∴![]()
![]()
![]() ,
,
∴![]() ,即
,即![]() ,
,
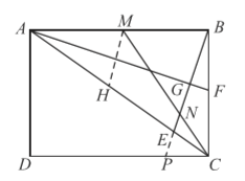
②延长![]() 交
交![]() 于
于![]() ,
,
∵四边形ABCD为矩形,
∴AB∥DC,
∴∠NMB=∠NCP,∠NPC=∠NBM,
∴![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
∴∠PGF=∠ABF,
又∵∠AFB=∠GFB,
∴![]()
∵∠ABF=∠BCP
∴![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.

 名校课堂系列答案
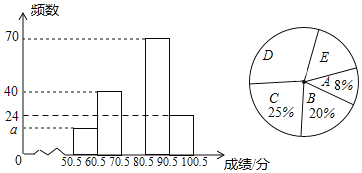
名校课堂系列答案【题目】为做好新型肺炎疫情防控,某街道组织社区200名志愿者开展新型肺炎疫情排查与宣传教育志愿服务活动,为了了解18~68岁各年龄段志愿者对本次新型肺炎疫情排查与宣传教育志愿服务的参与程度,随机选取了100名年龄在该范围内的志愿者进行了调查,并将收集到的数据制成了尚不完整的频数分布表,如下所示:
组别 | 年龄段 | 频数(人数) | 频率 |
第1组 |
| 5 | 5% |
第2组 |
|
| 25% |
第3组 |
| 35 | |
第4组 |
| 20 |
|
第5组 |
| 15 | 15% |
(1)请直接写出![]() _________,
_________,![]() _________.
_________.
(2)现该市有18~68岁的志愿者约有10000人,求第3组年龄段的志愿者人数约有多少?
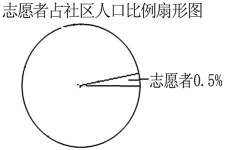
(3)如果这200名志愿者在该社区所占的比例如扇形统计图所示,求该社区估计有多少人?
(4)社区的部分果农、菜农自发踊跃捐助了一车的水果和蔬菜共8吨慰问社区志愿者助力社区疫情防控,其中定向捐助每个志愿者的水果与蔬菜之比是3:1,求该社区每个志愿者将分别得到多少千克的水果与蔬菜?
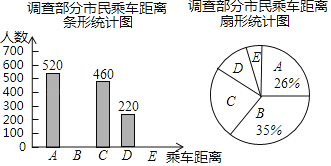
【题目】长春地铁一号线于2017年6月30日正式开通.运营公司根据乘车距离制定了不同的票价类别(见对照表).为了解乘客的乘车距离,运营公司随机选取了一部分经常需要乘车的市民进行了调查统计,绘制了两幅不完整的统计图.请你根据图表中提供的信息解答以下问题:
(1)本次抽样调查的人数是_________人.
(2)补全条形统计图.
(3)运营公司估计这条地铁专线通车后每天的客流量约为10万人,请你估算运营公司的日营业额.
类别 | 乘车距离d(公里) | 票价 |
A | 0<d≤7 | 2 |
B | 7<d≤13 | 3 |
C | 13<d≤19 | 4 |
D | 19<d≤27 | 5 |
E | 27<d≤35 | 6 |
票价类别与乘车距离对照表