题目内容
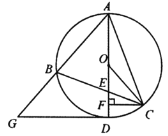
【题目】如图,点C、A、M、N在同一条直线l上.其中,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形
,四边形![]() 为正方形,且
为正方形,且![]() ,将等腰
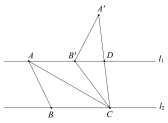
,将等腰![]() 沿直线l向右平移.若起始位置为点A与点M重合,终止位置为点C与点N重合.设点A平移的距离为x,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )
沿直线l向右平移.若起始位置为点A与点M重合,终止位置为点C与点N重合.设点A平移的距离为x,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )

A.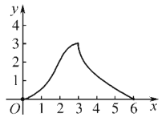 B.
B.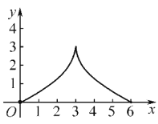
C.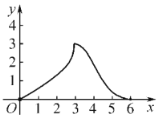 D.
D.
【答案】D
【解析】
分![]() ,
,![]() ,
,![]() 三种情况讨论,分别求得其函数关系式,利用数形结合的思想即可判断.
三种情况讨论,分别求得其函数关系式,利用数形结合的思想即可判断.
∵△ABC是等腰直角三角形,
作BO⊥直线![]() 于O,
于O,
则OA=OB=OC=2,
当![]() 时,如图:
时,如图:
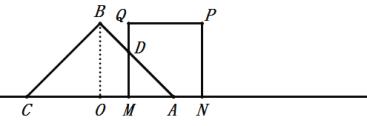
![]() ,
,
∴![]() ,
,
![]() ,开口向上的抛物线;
,开口向上的抛物线;
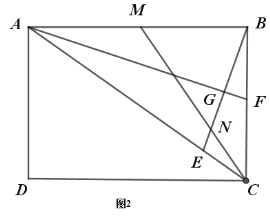
当![]() 时,如图:
时,如图:
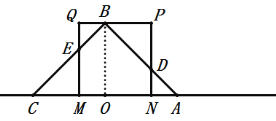
![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
![]() ,开口向下的抛物线;
,开口向下的抛物线;
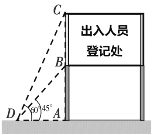
当![]() 时,如图:
时,如图:

![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,开口向上的抛物线;
,开口向上的抛物线;
综上,前后两段是开口向上的抛物线,中间一段是开口向下的抛物线,只有选项D符合,
故选:D.

练习册系列答案
相关题目
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
文文根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是文文的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是__________________;
的自变量x的取值范围是__________________;
(2)下表是y与x的几组对应值:
x | … |
|
|
|
|
| 0 |
| 1 |
| 2 | 3 | … |
y | … |
| 5 |
|
|
| 1 |
|
|
|
|
| … |
则m的值为____________;
(3)如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
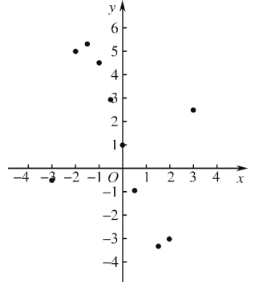
(4)请你根据探究二次函数与一元二次方程关系的经验,结合图象直接写出方程![]() 的正数根约为____________.(结果精确到0.1)
的正数根约为____________.(结果精确到0.1)