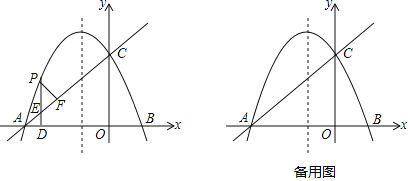Question

【题目】已知：是经过点A的一条直线，点C是直线左侧的一个动点，且满足，连接，将线段绕点C顺时针旋转60°，得到线段，在直线上取一点B，使．

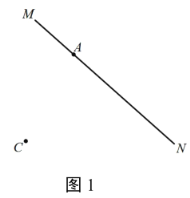
（1）若点C位置如图1所示．

①依据题意补全图1；

②求证：；

（2）连接，写出一个的值，使得对于任意一点C，总有，并证明．

Answer 1

【答案】（1）①图见解析；②证明见解析；（2）时，对于任意一点C，总有；证明见解析．

【解析】

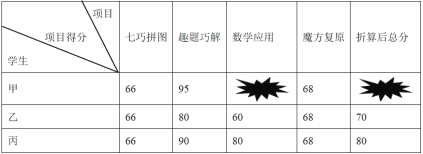
（1）①在AC右侧作等边三角形ACD，即可得线段，在作的外接圆交直线MN与B，连接DB即可补全图形；

②根据四边形内角和等于360°结合，即可得出，由同角的补角相等即可证明结论；

（2）连接，在直线上截取，连接，可得，进而是等边三角形，即得．

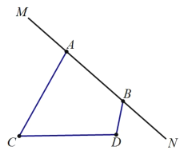
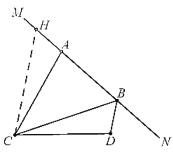
解：（1）① 补全图形，如图：

②证明：∵

∴

∵

∴

在四边形中，

∵

∴

（2）时，对于任意一点C，总有

证明：连接，在直线上截取，连接，

∵

∴

∴

∴

∴

∴是等边三角形．

∴．