题目内容
【题目】新华商场销售某种冰箱，每台进货价为2500元．市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台．商场要想使这种冰箱的销售利润平均每天达到5000元，设每台冰箱的定价为x元，则x满足的关系式为（ ）
A. (x2500)(8+4×
)=5000 B. (2900x2500)(8+4×)=5000
C. (x2500)(8+4×
)=5000 D. (2900x)(8+4×)=5000
【答案】C
【解析】
销售利润=一台冰箱的利润×销售冰箱数量，一台冰箱的利润=售价﹣进价，降低售价的同时，销售量就会提高，“一减一加”，根据每台的盈利×销售的件数=5000元，即可列方程求解．
设每台冰箱的定价应为x元，根据题意得：
（x﹣2500）（8+
4）=5000
故选C．
练习册系列答案
相关题目
【题目】如图，已知R t△ABC，∠ABC＝90°，以直角边AB为直径作O，交斜边AC于点D，连结BD．
（1）若AB＝3，BC＝4，求边BD的长；
（2）取BC的中点E，连结ED，试证明ED与⊙O相切．
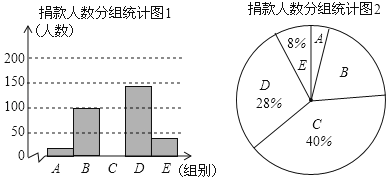
【题目】昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款人数的比为1：5．
组别 | 捐款额x/元 | 人数 |
A | 1≤x＜10 | a |
B | 10≤x＜20 | 100 |
C | 20≤x＜30 | |
D | 30≤x＜40 | |
E | 40≤x＜50 |
请结合以上信息解答下列问题．
（1）a＝ ，本次调查样本的容量是 ；
（2）先求出C组的人数，再补全“捐款人数分组统计图1”；
（3）根据统计情况，估计该校参加捐款的4500名学生有多少人捐款在20至40元之间．
