题目内容
【题目】大双，小双的妈妈申购到一张北京奥运会的门票，兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球，各自设计一种游戏确定谁去．
大双：A袋中放着分别标有数字1，2，3的三个小球，B袋中放着分别标有数字4，5的两个小球，且都已各自搅匀，小双蒙上眼睛从两个口袋中各取出1个小球，若两个小球上的数字之积为偶数，则大双得到门票；若积为奇数，则小双得到门票．
小双：口袋中放着分别标有数字1，2，3的三个小球，且已搅匀，大双，小双各蒙上眼睛有放回地摸1次，大双摸到偶数就记2分，摸到奇数记0分；小双摸到奇数就记1分，摸到偶数记0分，积分多的就得到门票．（若积分相同，则重复第二次．）
（1）大双设计的游戏方案对双方是否公平？请你运用列表或树状图说明理由；
（2）小双设计的游戏方案对双方是否公平？不必说理．
【答案】（1）不公平．理由参见解析；（2）不公平．
【解析】
试题分析：游戏是否公平，关键要看游戏双方获胜的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等．
试题解析：（1）大双的设计游戏方案不公平．可能出现的所有结果列表如下：
A袋 积 B袋 | 1 | 2 | 3 |
4 | 4 | 8 | 12 |
5 | 5 | 10 | 15 |
或列树状图如下：
∴P（大双得到门票）=P（积为偶数）=
=
，P（小双得到门票）=P（积为奇数）=
，∵
≠
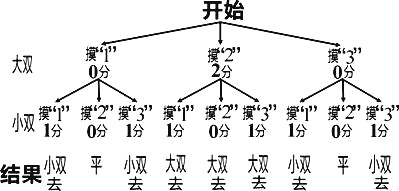
，∴大双的设计方案不公平．（2）小双的设计方案不公平．参考：可能出现的所有结果列树状图如下：
练习册系列答案
相关题目
