题目内容
【题目】如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠COB的度数. 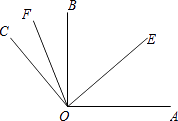
【答案】解:∵OE平分∠AOB,OF平分∠BOC, ∴∠BOE= ![]() ∠AOB=
∠AOB= ![]() ×90°=45°,∠COF=∠BOF=
×90°=45°,∠COF=∠BOF= ![]() ∠BOC,
∠BOC,
∵∠BOF=∠EOF﹣∠BOE=60°﹣45°=15°,
∴∠BOC=2∠BOF=30°;
∠AOC=∠BOC+∠AOB=30°+90°=120°
【解析】根据角平分线的定义得到∠BOE= ![]() ∠AOB=45°,∠COF=∠BOF=
∠AOB=45°,∠COF=∠BOF= ![]() ∠BOC,再计算出∠BOF=∠EOF﹣∠BOE=15°,然后根据∠BOC=2∠BOF,∠AOC=∠BOC+∠AOB进行计算.
∠BOC,再计算出∠BOF=∠EOF﹣∠BOE=15°,然后根据∠BOC=2∠BOF,∠AOC=∠BOC+∠AOB进行计算.
【考点精析】利用角的平分线对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】学校体育课进行定点投篮比赛,10位同学参加,每人连续投5次,投中情况统计如下:
投中球数量(个) | 2 | 3 | 4 | 5 |
人数(人) | 1 | 4 | 3 | 2 |
这10位同学投中球数量的众数和中位数分别是( )
A. 4, 2 B. 3,4 C. 2,3.5 D. 3,3.5