题目内容
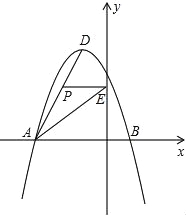
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
【答案】(1)、y=﹣x2﹣2x+3;D(-1,4);(2)、S﹣x2﹣3x(﹣3<x<﹣1),当x=﹣![]() 时,S取最大值
时,S取最大值![]() ;(3)、∴P′(
;(3)、∴P′(![]() ,
,![]() ),不在抛物线上
),不在抛物线上
【解析】
试题分析:(1)、由抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,则代入求得a,b,c,进而得解析式与顶点D.(2)、由P在AD上,则可求AD解析式表示P点.由S△APE=![]() PEyP,所以S可表示,进而由函数最值性质易得S最值.(3)、由最值时,P为(﹣
PEyP,所以S可表示,进而由函数最值性质易得S最值.(3)、由最值时,P为(﹣![]() ,3),则E与C重合.画示意图,P'过作P'M⊥y轴,设边长通过解直角三角形可求各边长度,进而得P'坐标.判断P′是否在该抛物线上,将xP'坐标代入解析式,判断是否为yP'即可.
,3),则E与C重合.画示意图,P'过作P'M⊥y轴,设边长通过解直角三角形可求各边长度,进而得P'坐标.判断P′是否在该抛物线上,将xP'坐标代入解析式,判断是否为yP'即可.
试题解析:(1)、∵抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,
∴ , 解得:
, 解得: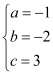 , ∴解析式为y=﹣x2﹣2x+3
, ∴解析式为y=﹣x2﹣2x+3
∵﹣x2﹣2x+3=﹣(x+1)2+4, ∴抛物线顶点坐标D为(﹣1,4).
(2)、∵A(﹣3,0),D(﹣1,4), ∴设AD为解析式为y=kx+b,有![]() , 解得
, 解得![]() ,
,
∴AD解析式:y=2x+6, ∵P在AD上, ∴P(x,2x+6),
∴S△APE=![]() PEyP=
PEyP=![]() (﹣x)(2x+6)=﹣x2﹣3x(﹣3<x<﹣1),当x=﹣
(﹣x)(2x+6)=﹣x2﹣3x(﹣3<x<﹣1),当x=﹣![]() 时,S取最大值
时,S取最大值![]() .
.
(3)、如图1,设P′F与y轴交于点N,过P′作P′M⊥y轴于点M,
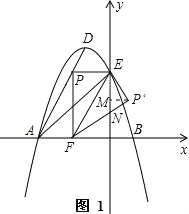
∵△PEF沿EF翻折得△P′EF,且P(﹣![]() ,3), ∴∠PFE=∠P′FE,PF=P′F=3,PE=P′E=
,3), ∴∠PFE=∠P′FE,PF=P′F=3,PE=P′E=![]() ,
,
∵PF∥y轴, ∴∠PFE=∠FEN, ∵∠PFE=∠P′FE, ∴∠FEN=∠P′FE, span>∴EN=FN,
设EN=m,则FN=m,P′N=3﹣m. 在Rt△P′EN中, ∵(3﹣m)2+(![]() )2=m2, ∴m=
)2=m2, ∴m=![]() .
.
∵S△P′EN=![]() P′NP′E=
P′NP′E=![]() ENP′M, ∴P′M=
ENP′M, ∴P′M=![]() . 在Rt△EMP′中
. 在Rt△EMP′中
∵EM=![]() , ∴OM=EO﹣EM=
, ∴OM=EO﹣EM=![]() , ∴P′(
, ∴P′(![]() ,
,![]() ).
).
当x=![]() 时,y=﹣(
时,y=﹣(![]() )2﹣2
)2﹣2![]() +3=0.39≠
+3=0.39≠![]() , ∴点P′不在该抛物线上.
, ∴点P′不在该抛物线上.

 阅读快车系列答案
阅读快车系列答案【题目】李老师布置了两道解方程的作业题:
(1)选用合适的方法解方程:(x+1)(x+2)=6;
(2)用配方法解方程:2x2+4x-5=0.
以下是小明同学的作业:
(1)解:由(x+1)(x+2)=6, | (2)解:由2x2+4x-5=0, |
得x+1=2,x+2=3, | 得2x2+4x=5, |
所以x1=1,x2=1. | x2+2x= |
x2+2x+1= | |
(x+1)2= | |
x+1=± | |
x1=-1+ |
请你帮小明检查他的作业是否正确,把不正确的改正过来.
