题目内容
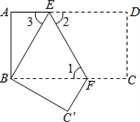
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=60°,求∠3的度数;
(2)求证:BE=BF
(3)若AB=6,AD=12,求△BEF的面积.
【答案】(1)60°;(2)证明见解析;(3)7.5
【解析】试题分析:(1)根据平行线的性质、翻转变换的性质解答;
(2)根据等腰三角形的性质证明;
(3)根据翻转变换的性质、勾股定理计算即可.
试题解析:(1)∵AD∥BC,
∴∠2=∠1=60°,
由翻转变换的性质可知,∠BEF=∠2=60°,
∴∠3=60°;
(2)证明:∵∠BEF=∠1=60°,
∴BE=BF;
(3)由翻转变换的性质可知,BE=DE=12-AE,
由勾股定理得,BE2=AB2+AE2,即(12-AE)2=62+AE2,
解得,AE=4.5,
则BF=BE=7.5,
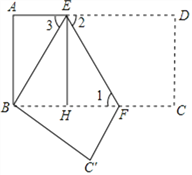
∵四边形ABHE是矩形,
∴EH=AB=6,
∴△BEF的面积=![]() ×BF×EH=22.5.
×BF×EH=22.5.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目