题目内容
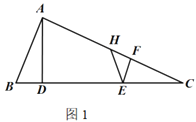
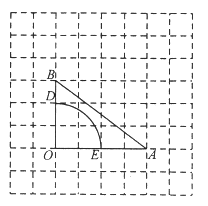
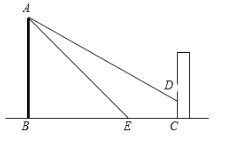
【题目】如图,某公园内有一座古塔AB,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD.中午12时太阳光线与地面的夹角为45°,此时塔尖A在地面上的影子E与墙角C的距离为15米(B、E、C在一条直线上),求塔AB的高度.(结果精确到0.01米)
参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,![]() .
.
【答案】塔高AB约为32.99米.
【解析】
过点D作DH⊥AB,垂足为点H,设AB=x,则 AH=x﹣3,解直角三角形即可得到结论.
解:过点D作DH⊥AB,垂足为点H.
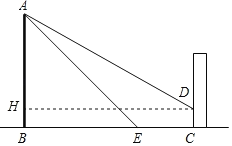
由题意,得 HB = CD = 3,EC = 15,HD = BC,∠ABC =∠AHD = 90°,
∠ADH = 32°.
设AB = x,则 AH = x – 3.
在Rt△ABE中,由 ∠AEB = 45°,得 ![]() .
.
∴ EB = AB = x.∴ HD = BC = BE + EC = x + 15.
在Rt△AHD中,由 ∠AHD = 90°,得 ![]() .
.
即得 ![]() .
.
解得 ![]() .
.
∴ 塔高AB约为32.99米.

练习册系列答案
相关题目