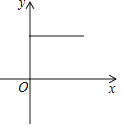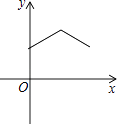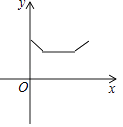题目内容
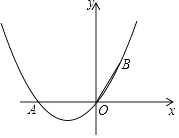
【题目】如图,在△ABC中∠ABC=90°,∠A=30°,BC=2cm,动点P以3cm/s的速度由A沿射线AC方向运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交直线AB于D,则当运动时间为s时,△ADP是等腰三角形. 
【答案】![]() 或3或
或3或 ![]()
【解析】解:∵∠ABC=90°,∠A=30°,BC=2cm, ∴AC=2BC=4cm,AB=ACcosA=4× ![]() =2
=2 ![]() cm,
cm,
设运动时间为t,则AP=3t,BQ=t,
①当PA=PD时,如图1,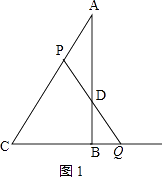
则∠BDQ=∠PDA=∠A=30°,
∴∠C=∠CPQ=60°,DQ=2BQ=2t,
∴PQ=PC=AC﹣AP=4﹣3t,
∴PD=PQ﹣DQ=4﹣3t﹣2t=4﹣5t,
则4﹣5t=3t,
解得:t= ![]() ;
;
②当AP=AD时,如图2,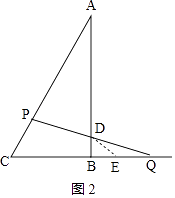
则∠ADP=∠BDQ= ![]() =75°,
=75°,
∴∠DQB=15°,
以DQ为边在∠BDQ内部作∠EDQ=∠DQB=15°,
∴设DE=QE=x,∠DEB=30°,
∴BE=BQ﹣EQ=t﹣x,
由cos∠DEB= ![]() 得
得 ![]() ,
,
解得:x=2(2﹣ ![]() )t,即DE=2(2﹣
)t,即DE=2(2﹣ ![]() )t,
)t,
∴BD=DEsin∠DEB=(2﹣ ![]() )t,
)t,
∴AD=AB﹣BD=2 ![]() ﹣(2﹣
﹣(2﹣ ![]() )t,
)t,
由AP=AD得3t=2 ![]() ﹣(2﹣
﹣(2﹣ ![]() )t,
)t,
解得:t= ![]() ;
;
③当DA=DP时,如图3,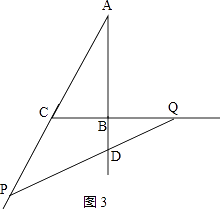
则∠A=∠APD=30°,
∴∠CQP=∠ACB﹣∠APD=30°,
∴∠CQP=∠APD=30°,
∴CP=CQ,则3t﹣4=2+t,
解得:t=3,
综上,当运动时间为 ![]() 或3或
或3或 ![]() s时,△ADP是等腰三角形.
s时,△ADP是等腰三角形.
【考点精析】本题主要考查了等腰三角形的判定的相关知识点,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能正确解答此题.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案