题目内容
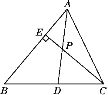
【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD、CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
【答案】123°.
【解析】
试题在直角三角形BCE中∠BCE=40°,可求出∠B=50°,由三角形内角和可求出∠BCA的度数;由AD是∠BAC的角平分线易求∠ADC的度数,再由CE⊥AB易求∠ACE的度数,从而可求∠APC的度数.
试题解析:∵AD是△ABC的角平分线,∠BAC=66°,
∴∠DAC=∠BAD=33°,
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∠ACB=180°-50°-66°=64°;
∴∠ADC=180°-64°-33°=83°,∠APC=123°
考点: 1.角平分线;2.三角形的内角和.

练习册系列答案
相关题目
【题目】2017年5月,举世瞩目的“一带一路”国际合作高峰论坛在北京举行.为了让学生更深刻地了解这一普惠世界的中国创举,某校组织八年级甲班和乙班的学生开展“一带一路”知识竞赛活动.现场决赛时,甲班和乙班分别选5名同学参加比赛,成绩如图所示:

(1)根据上图将计算结果填入下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | _____ | _____ |
乙班 | 8.5 | ______ | 10 | 1.6 |
(2)你认为哪个班的成绩较好?为什么?




