题目内容
【题目】如图,在直角坐标系中,点A的坐标为(﹣2,0),OB=OA,且∠AOB=120°.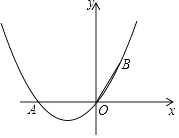
(1)求经过A,O,B三点的抛物线的解析式.
(2)在(1)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M,N使得A,O,M,N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,
在Rt△OBD中,∠ODB=90°,∠OBD=30°
∴OD=1,DB= ![]()
∴点B的坐标是(1, ![]() ).
).
设所求抛物线的解析式为y=ax2+bx+c,
由已知可得: 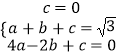 ,
,
解得: 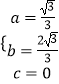
∴所求抛物线解析式为y= ![]() .
.
(2)
解:存在,
∵△BOC的周长=OB+BC+CO,
又∵OB=2
∴要使△BOC的周长最小,必须BC+CO最小,
∵点O和点A关于对称轴对称
∴连接AB与对称轴的交点即为点C,
且有OC=OA
此时△BOC的周长=OB+BC+CO=OB+BC+AC;
点C为直线AB与抛物线对称轴的交点
设直线AB的解析式为y=kx+b,
将点A(﹣2,0),B(1, ![]() )分别代入,得:
)分别代入,得:
![]() ,
,
解得: 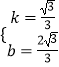 ,
,
∴直线AB的解析式为y= ![]() x+
x+ ![]()
当x=﹣1时,y= ![]() ,
,
∴所求点C的坐标为(﹣1, ![]() );
);
(3)
解:如图,
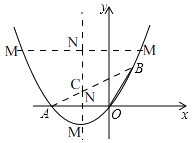
①当以OA为对角线时,
OA与MN互相垂直且平分
∴点M(﹣1,﹣ ![]() ),
),
②当以OA为边时
OA=MN且OA∥MN
即MN=2,MN∥x轴
设N(﹣1,t)
则M(﹣3,t)或(1,t)
将M点坐标代入y= ![]() .
.
∴t= ![]()
∴M(﹣3, ![]() )或(1,
)或(1, ![]() )
)
综上:点M的坐标为:M(﹣1,﹣ ![]() )或(﹣3,
)或(﹣3, ![]() )或(1,
)或(1, ![]() ).
).
【解析】(1)先确定出点B坐标,再用待定系数法即可;(2)先判断出使△BOC的周长最小的点C的位置,再求解即可;(3)分OA为对角线和为边两种情况进行讨论计算.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?