题目内容
【题目】甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1000米,甲超出乙150米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点还有_____米.
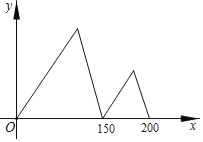
【答案】50
【解析】
乙从开始一直到终点,行1000米用时200秒,因此乙的速度为1000÷200=5米/秒,甲停下来,乙又走150÷5=30秒才与甲第一次会和,第一次会和前甲、乙共同行使150-30=120秒,从起点到第一次会和点的距离为5×150=750米,因此甲的速度为750÷120=6.25米/秒,甲行完全程的时间为1000÷6.25=160秒,甲到终点时乙行驶时间为160+30=190秒,因此乙距终点还剩200-190=10秒的路程,即10×5=50米.
乙的速度为:1000÷200=5米/秒,从起点到第一次会和点距离为5×150=750米,
甲停下来到乙到会和点时间150÷5=30秒,之前行驶时间150﹣30=120秒,
甲的速度为750÷120=6.25米/秒,
甲到终点时乙行驶时间1000÷6.25+30=190秒,
还剩10秒路程,即10×5=50米,
故答案为50米.

【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
【题目】甲、乙两名射击选手在10次射击训练中的成绩统计图(部分)如图所示:
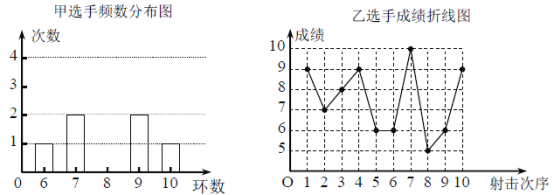
教练根据甲、乙两名射击选手的成绩绘制了如下数据分析表:
选手 | 平均数 | 中位数 | 众数 | 方差 |
甲 |
| 8 | 8 | c |
乙 | 7. 5 |
| 6和9 | 2. 65 |
根据以上信息,请解答下面的问题:
(1)补全甲选手10次成绩频数分布图;
(2)求![]() 的值;
的值;
(3)教练根据两名选手的10次成绩,决定选择甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).