题目内容
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
【答案】(1)y与x的函数关系式为y=-x+150;(2)该批发商若想获得4000元的利润,应将售价定为70元;(3)该产品每千克售价为85元时,批发商获得的利润w(元)最大,此时的最大利润为4225元.
【解析】试题分析:(1)根据图表中的各数可得出y与x成一次函数关系,从而结合图表的数可得出y与x的关系式.
(2)根据想获得4000元的利润,列出方程求解即可;
(3)根据批发商获得的总利润w(元)=售量×每件利润可表示出w与x之间的函数表达式,再利用二次函数的最值可得出利润最大值.
解:(1)设y与x的函数关系式为y=kx+b(k≠0),根据题意得
![]() ,
,
解得![]() .
.
故y与x的函数关系式为y=﹣x+150;
(2)根据题意得
(﹣x+150)(x﹣20)=4000,
解得x1=70,x2=100>90(不合题意,舍去).
故该批发商若想获得4000元的利润,应将售价定为70元;
(3)w与x的函数关系式为:
w=(﹣x+150)(x﹣20)
=﹣x2+170x﹣3000
=﹣(x﹣85)2+4225,
∵﹣1<0,
∴当x=85时,w值最大,w最大值是4225.
∴该产品每千克售价为85元时,批发商获得的利润w(元)最大,此时的最大利润为4225元.

【题目】某校举行“汉字听写”比赛,全体学生都参与,每名学生听写39个汉字,比赛结束后,学校随机抽查了部分学生的听写结果,绘制成如下所示的统计表(不完整)和如图所示的统计图(不完整) .请根据题意解答下列问题.
组别 | 正确的个数x | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
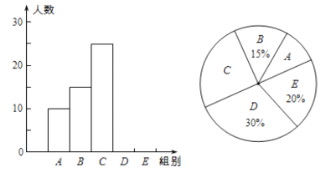
(1)统计表中的m=__,n=___;
(2)请补全频数分布直方图:
(3)在扇形统计图中,C组所对应扇形的圆心角的度数是______ ;
(4)已知该校共有1260名学生,如果听写汉字正确的个数少于24定为不合格,那么该校本次比赛不合格的学生人数大约是多少?