题目内容
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
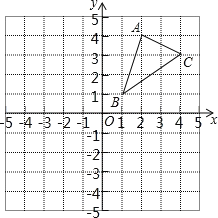
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
(4)在x轴上有一点P,PA+PB的值最小,请直接写出点P的坐标
【答案】(1)根A1(2,4),B1(1,1),C1(4,3)(2)图形见解析(3) ![]() (4)(1.2,0)
(4)(1.2,0)
【解析】试题分析:(1)利用关于x轴对称点的横坐标相等,纵坐标互为相反数可先找出点A1、B1、C1的坐标,然后画出图形即可;
(2)利用旋转的性质可确定出点A2、C2的坐标;
(3)先求出BC的长,然后利用弧长公式进行计算即可;
(4)连接A1B,与x轴相交于点P,则此时PA+PB的值最小.利用待定系数法求出直线A1B的解析式,然后求出与x轴的交点即可.
试题解析:
(1)根据关于x轴对称点的坐标特点可知:A1(2,4),B1(1,1),C1(4,3),
如下图:连接A1、B1、C1即可得到△A1B1C1.
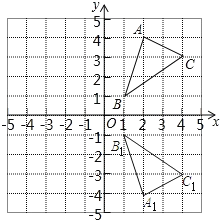
(2)如图:
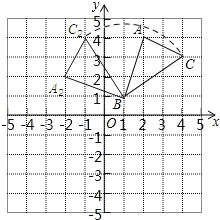
(3)由两点间的距离公式可知:BC=![]() ,
,
∴点C旋转到C2点的路径长=![]()
(4)连接A1B,与x轴相交于点P,则此时PA+PB的值最小.
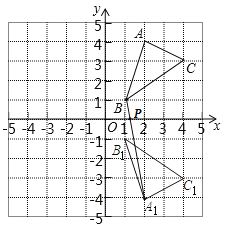
设直线A1B的解析式为y=kx+b,
则![]() ,
,
解得![]() ,
,
∴直线A1B的解析式为y=-5x+6,
令y=0,则-5x+6=0,
x=1.2,
所以点P的坐标为(1.2,0).

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?