题目内容
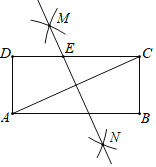
【题目】如图，在矩形ABCD中，按以下步骤作图：①分别以点A和点C为圆心，以大于
AC的长为半径作弧，两弧相交于点M和N；②作直线MN交CD于点E，若AB=8，AD=6，则EC=_____________．
【答案】
【解析】
连接EA，如图，利用基本作图得到MN垂直平分AC，所以EC=EA，设CE=x，则AE=x，DE=8-x，根据勾股定理得到62+（8-x）2=x2，然后解方程求出x即可．
解：连接EA，如图，
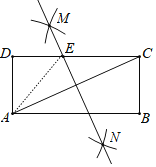
由作图得到MN垂直平分AC，
∴EC=EA，
∵四边形ABCD为矩形，
∴CD=AB=8，∠D=90°，
设CE=x，则AE=x，DE=8-x，
在Rt△ADE中，62+（8-x）2=x2，解得x=，
即CE的长为．
故答案为．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
【题目】某电路检修小组在东西方向的一道路上检修用电线路，检修车辆从该道路
处出发，如果规定检修车辆向东行驶为正，向西行驶为负，某一天施工过程中七次车辆行驶记录如下（单位：千米）：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
（
）问检修小组收工时在的哪个方位？距处多远？
（2）若检修车辆每千米耗油
升，每升汽油需
元，问这一天检修车辆所需汽油费多少元？
