��Ŀ����
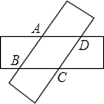
����Ŀ����ͼ���������߶�AB��2(��λ����)���߶�CD��4(��λ����)����A�������ϱ�ʾ�����ǣ�10����C�������ϱ�ʾ������16.���߶�AB��ÿ��6����λ���ȵ��ٶ����������˶���ͬʱ�߶�CD��ÿ��2����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt s.
(1)����B���C����ʱ����A����D�������ϱ�ʾ�����ֱ�Ϊ________��
(2)��tΪ��ֵʱ����B�պ����߶�CD���е��غϣ�
(3)���˶���BC��8(��λ����)ʱ�������ʱ��B�������ϱ�ʾ������
![]()
���𰸡�(1)8��14(2)��tΪ![]() ʱ����B�պ����߶�CD���е��غ�(3) 4��16
ʱ����B�պ����߶�CD���е��غ�(3) 4��16
��������
�������ͼʾ����B���ʾ�����ǩ�8����D��ʾ������20��
��1�����ٶ���ʱ��=�����г����̣�6+2��t=24��������t=3���ݴ˿�����õ�A��D�ƶ�������ʾ������
��2��C��D���е�����ʾ������18���������⣬�ã�6+2��t=26��������t��ֵ��
��3����Ҫ�������ۣ�����B�ڵ�C�������Ҳ����������
����������⣺��ͼ����AB=2����λ���ȣ�����A�������ϱ�ʾ�����ǩ�10����B���ʾ�����ǩ�10+2=��8��
�����߶�CD=4����λ���ȣ�����C�������ϱ�ʾ������16������D��ʾ������20��
��1���������⣬��
��6+2��t=|��8��16|=24����8t=24����ã�t=3��
���A��ʾ������6��3��|��10|=8����D�������ϱ�ʾ������20��2��3=14��
�ʴ�Ϊ��8��14��
��2��C��D���е�����ʾ������18���������⣬��
��6+2��t=26�����t=![]() ��
��
�𣺵�tΪ![]() ʱ����B�պ����߶�CD���е��غϣ�
ʱ����B�պ����߶�CD���е��غϣ�
��3������B�ڵ�C�����ʱ��������ã�
��6+2��t+8=24�����t=2����ʱ��B������������ʾ������4��
����B�ڵ�C���Ҳ�ʱ��������õ���
��6+2��t=32�����t=4����ʱ��B������������ʾ������24��8=16��
������������B������������ʾ������4��16��

����Ŀ��ij�ּ�ʱ��������0��00ʱ�̵�ȼ����������ʣ��ij���h��cm����ȼ�յ�ʱ��x��h��֮����һ�κ�����ϵ��h��x��һ���Ӧ��ֵ�����ʾ��
ȼ�յ�ʱ��x��h�� | �� | 3 | 4 | 5 | 6 | �� |
ʣ��ij���h��cm�� | �� | 210 | 200 | 190 | 180 | �� |
��1��д����������0��00ʱ�̵�Ȼ����ʣ��ij���h��cm����ȼ��ʱ��x��h���ĺ�����ϵʽ�������ͺ�������ʽ��x��ϵ�����������ʵ�����壻
��2��ͨ������˵����������ʣ��ij���Ϊ125cmʱ��ʱ�̣�