题目内容
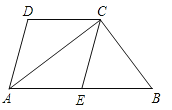
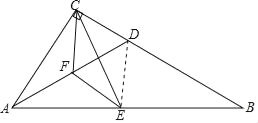
【题目】如图,Rt△ABC中,∠ACB=90°,D是边BC上一点,点E、F分别是线段AB、AD中点,联结CE、CF、EF.
(1)求证:△CEF≌△AEF;
(2)联结DE,当BD=2CD时,求证:AD=2DE.

【答案】(1)见解析;(2)见解析.
【解析】
(1)在直角三角形ABC中,E为斜边AB的中点,利用斜边上的中线等于斜边的一半得到CE=AE,在直角三角形ACD中,F为斜边AD的中点,利用斜边上的中线等于斜边的一半得到AF=CF,再由EF=EF,利用SSS即可得证;
(2)由EF为三角形ABD的中点,利用中位线定理得到EF与BD平行,EF等于BD的一半,再由BD=2DC,等量代换得到EF=CD,再由EF与CD平行,得到四边形CEFD为平行四边形,可得出DE=CF,再由CF=AF,等量代换得到DE=AF.
证明:(1)∵∠ACB=90°,且E线段AB中点,
∴CE=![]() AB=AE,
AB=AE,
∵∠ACD=90°,F为线段AD中点,
∴AF=CF=![]() AD,
AD,
在△CEF和△AEF中,
 ,
,
∴△CEF≌△AEF(SSS);
(2)连接DE,
∵点E、F分别是线段AB、AD中点,
∴EF=![]() BD,EF∥BC,
BD,EF∥BC,
∵BD=2CD,
∴EF=CD.
又∵EF∥BC,
∴四边形CFEDD是平行四边形,
∴DE=CF,
∵CF=AF=FD,
∴AD=2DE.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目