题目内容
【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
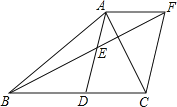
解:(1)如图①,延长AB到E,过点B作BF∥AC.
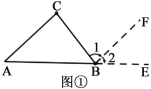
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
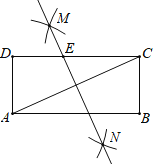
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”

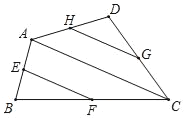
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .

【答案】(1)(2) 见解析;(3)540°
【解析】
(1)运用平行线的性质进行分析即可;(2)运用两次两直线平行,内错角相等即可;(3)连接EC、EB,转换成三个三角形的内角和即可.
解:(1)如图①,延长AB到E,过点B作BF∥AC.
∵BF∥AC(作图)
∴∠1=∠C(两直线平行,内错角相等)
∠2=∠A(两直线平行,同位角相等)
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
(2)如图②,过C作MN∥AB
∵MN∥AB
∴∠1=∠B,∠2=∠A(两直线平行,内错角相等)
又∵∠1+∠ACB+∠2=180°(平角的定义)
∴A+∠ABC+∠C=180°
(3)如图:连接EC、EB,

∵在△ABC、△ACD和△AED中,
∴∠BAC+∠B+∠ACB=180",∠DAC+∠ACD+∠ADC=180°∠DAE+∠E+∠ADE=180°
∴∠BAE+∠B+∠DCB+ ∠CDE+∠E
=∠BAC+∠CAD+∠DAE+∠BCA+∠ACD+∠ADE+∠ADC+∠B+∠E
=(∠BAC+∠B+∠ACB)+( ∠DAC+∠ACD+∠ADC)+( ∠DAE+∠E+∠ADE)
=540°

【题目】某厂为了检验甲、乙两车间生产的同一种零件的直径的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:(单位:![]() )
)
170~174 | 175~179 | 180~184 | 185~189 | |
甲车间 | 1 | 3 | 4 | 2 |
乙车间 | 0 | 6 | 2 | 2 |
(1)分别计算甲、乙两车间生产的零件直径的平均数;
(2)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(3)若该零件的直径在![]() 的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?