题目内容
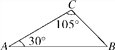
【题目】如图,已知AC=4,求AB和BC的长.
【答案】AB=2+2![]() ; BC=2
; BC=2![]()
【解析】试题分析:
根据三角形内角和不难求得∠B=45°. 由于∠A和∠B的角度值均为特殊角度值,所以可以利用AB边上的高(设该高为CD)将△ABC分成两个含有特殊角的直角三角形进行求解. 利用已知条件可以求解Rt△ADC,从而求得线段AD与CD的长. 由于线段CD为这两个直角三角形的公共边,并且已经求得∠B的值,所以Rt△CDB也是可解的. 解这个直角三角形,可以求得线段BC与BD的长,进而容易求得线段AB的长.
试题解析:

如图,过点C作CD⊥AB,垂足为D.
∵∠A=30°,AC=4,
∴在Rt△ADC中,
![]() ,
,
![]() ,
,
∵∠ACB=105°,∠A=30°,
∴在△ABC中,∠B=180°-∠A-∠ACB=180°-30°-105°=45°,
∵CD=2,
∴在Rt△CDB中,
![]() ,
,
![]() ,
,
∴AB=AD+BD=![]() .
.
综上所述,AB=![]() ,BC=
,BC=![]() .
.

练习册系列答案
相关题目