题目内容
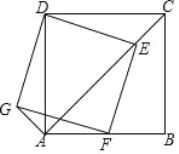
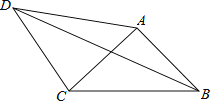
【题目】如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
【答案】![]() .
.
【解析】
试题根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案:
如答图,作AD′⊥AD,AD′=AD,连接CD′,DD′,
∵∠ABC=∠ACB=45°,∴BA=BC.
∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,
在△BAD与△CAD′中,∵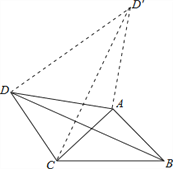 ,∴△BAD≌△CAD′(SAS).∴BD=CD′.
,∴△BAD≌△CAD′(SAS).∴BD=CD′.
在Rt△ADD′中,由勾股定理得![]() .
.
∵∠D′DA=∠ADC=45°,∴∠D′DC=90°.
在Rt△CDD′中,由勾股定理得![]() ,
,
∴BD=CD′=![]() .
.
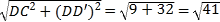

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目