Question

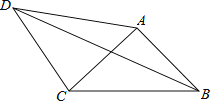
【题目】已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.

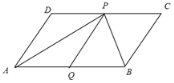
(1)求证:AP⊥PB;

(2)如果AD=5cm,AP=8cm,那么□ ABCD 的面积是多少?

Answer 1

【答案】（1）见解析；（2）48 cm2．

【解析】

（1）根据平行四边形性质得出AD∥CB，AB∥CD，推出∠DAB+∠CBA=180°，求出∠PAB+∠PBA=90°，在△APB中求出∠APB即可；

（2）根据平行四边形性质得出AD∥CB，AB∥CD，由已知QP∥AD可证四边形DAQP、PQBC是平行四边形，则 ， ，即□ ABCD 的面积=2 ，求出AD=DP=5，BC=PC=5，求出DC=10=AB，由勾股定理求出BP，求出，即可求出答案．

证明：（1）∵ABCD是平行四边形，
∴AD∥CB．∴∠DAB+∠CBA=180°．
又∵AP和BP分别平分∠DAB和∠CBA，
∴∠PAB+∠PBA=（∠DAB+∠CBA）=90°．
在△APB中，∵∠APB=180°-（∠PAB+∠PBA）=90°．
∴AP⊥PB；

（2）∵四边形ABCD是平行四边形，
∴AD∥CB，AB∥CD，

∵QP∥AD

∴四边形DAQP、PQBC是平行四边形，

∴ ， ，

∴□ ABCD 的面积=2 ，

∵AP平分∠DAB，
∴∠DAP=∠PAB，
∵AB∥CD，
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形，
∴AD=DP=5，
同理：PC=CB=5，
即AB=DC=DP+PC=10，
在Rt△APB中，AB=10，AP=8，
∴BP==6，
∴△ABP的面积为：×6×8=24（cm2）

∴□ ABCD 的面积=2=48 cm2．

故答案为：（1）见解析；（2）48 cm2．