题目内容
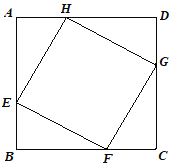
【题目】如图，正方形ABCD的边长为8cm，E、F、G、H分别是AB、BC、CD、DA上的动点，且AE=BF=CG=DH．则四边形EFGH面积的最小值是________cm2．
【答案】32
【解析】分析：根据正方形的性质结合已知可推出：△EAH≌△FBE≌△GCF≌△HDG，结合全等三角形的性质得到四边形EFGH是菱形；根据角度间关系容易得出∠HEF=90°，进而得到四边形EFGH是正方形，设AE=DH=x，则AH=8-x，在Rt△AEH中利用勾股定理可得：EH2=AE2+AH2，结合二次函数的最值解答即可.
详解：∵四边形ABCD是正方形，
∴∠BAD=∠ABC=∠BCD=∠CDA=90°，AB=BC=CD=DA.
∵AE=BF=CG=DH，
∴BE=CF=AH=DG，
∴△EAH≌△FBE≌△GCF≌△HDG，
∴EH=EF=FG=HG，∠AEH=∠BFE，
∴四边形EFGH是菱形.
∵∠BEF+∠BFE=90°，∠AEH=∠BFE，
∴∠BEF+∠AEH=90°，
∴∠HEF=90°.
∵四边形EFGH是菱形，∠HEF=90°，
∴四边形EFGH是正方形.
正方形EFGH的面积最小，则边长EF最小.
设AE=DH=x，则AH=8-x，
∵在Rt△AEH中，EH2=AE2+AH2=x2+(8-x)2=2x2-16x+64=2(x-4)2+32，
∴四边形EFGH面积的最小值为32cm2.
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
