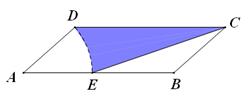
题目内容
如图所示, 是
是 的内接三角形,
的内接三角形, ,
,  为
为 中弧AB上一点,延长
中弧AB上一点,延长 至点
至点 ,使
,使 .
.

(1)求证: ;
;
(2)若 ,求证:
,求证: .
.
 是
是 的内接三角形,
的内接三角形, ,
,  为
为 中弧AB上一点,延长
中弧AB上一点,延长 至点
至点 ,使
,使 .
.
(1)求证:
 ;
;(2)若
 ,求证:
,求证: .
.(1)详见解析;(2)详见解析.
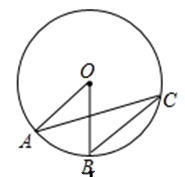
试题分析:(1)由题意知,⊿ABC和⊿ECD都是等腰三角形,根据“同弧所对的圆周角相等”可知,∠ABC=∠ADC,由此可得,∠ACE=∠BCD,结合已知条件,利用“SAS”可证⊿ACE≌⊿BCD,所以有AE=BD.(2)若AC⊥BC,则有(1)的结论可知,∠DCE=90°,DE=AD+BD,又已知CD=CE,所以三角形DCE是等腰直角三角形,DE=
 CD,所以得证.规律:在解决圆中的线段相等关系或角相等时,常常要借助于三角形全等.
CD,所以得证.规律:在解决圆中的线段相等关系或角相等时,常常要借助于三角形全等.
试题解析:证明:(1)由同弧所对的圆周角相等,知∠
 ∠
∠ .
.∵
 ,
,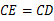 ,∴ ∠
,∴ ∠ ∠
∠ ∠
∠ ∠
∠ ,
,∴ ∠
 ∠
∠ ,
,∴∠DCE-∠ACD=∠ACB-∠ACD
即:∠
 ∠
∠ .
.又∵
 ,
,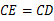 ,
,∴ △
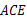 ≌△
≌△ . ∴
. ∴  5分
5分(2) ∵
 ,∴
,∴ 
∵
 ,∴ ∠
,∴ ∠ , ∴ ∠
, ∴ ∠ ∠
∠ .
.由勾股定理,得

又∵
 , ∴
, ∴  ,∴
,∴  ,
,∴
 . 10分
. 10分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

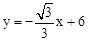 分别与x轴、y轴相交于B、A两点.点C在射线BA上以3厘米/秒的速度运动,以C点为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,过点P作直线l∥x轴.若点C与点P同时从点B、点O开始运动,设运动时间为t秒,则在整个运动过程中直线l与⊙C最后一次相切时t= 秒.
分别与x轴、y轴相交于B、A两点.点C在射线BA上以3厘米/秒的速度运动,以C点为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,过点P作直线l∥x轴.若点C与点P同时从点B、点O开始运动,设运动时间为t秒,则在整个运动过程中直线l与⊙C最后一次相切时t= 秒.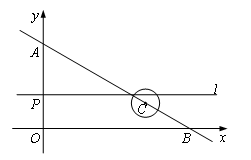
 ).
).