题目内容
△ABC内接于⊙O中,AD平分∠BAC交⊙O于D.

(1)如图1,连接BD,CD,求证:BD=CD
(2)如图2,若BC是⊙O直径,AB=8,AC=6,求BD长
(3)如图,若∠ABC的平分线与AD交于点E,求证:BD=DE

(1)如图1,连接BD,CD,求证:BD=CD
(2)如图2,若BC是⊙O直径,AB=8,AC=6,求BD长
(3)如图,若∠ABC的平分线与AD交于点E,求证:BD=DE
(1)答案见试题解析;(2)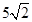 ;(3)答案见试题解析.
;(3)答案见试题解析.
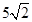 ;(3)答案见试题解析.
;(3)答案见试题解析.试题分析:(1)由AD平分∠BAC交⊙O于D,可得
 =
= ,即可证得BD=CD;
,即可证得BD=CD;(2)由BC是⊙O直径,根据直径所对的圆周角是直角,可得∠BAC=∠BDC=90°,然后由勾股定理求得答案;
(3)由∠ABC的平分线与AD交于点E,利用三角形外角的性质与圆周角定理可求得∠BED=∠DBE,继而可证得BD=DE.
试题解析:(1)证明:∵AD平分∠BAC交⊙O于D,∴
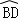 =
= ,∴BD=CD;
,∴BD=CD;(2)解:∵BC是⊙O直径,∴∠BAC=∠BDC=90°,∵AB=8,AC=6,∴BC=
 =10,∵BD=CD,∴BD=
=10,∵BD=CD,∴BD=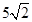 ;
;(3)证明:∵AD平分∠BAC交⊙O于D,∠ABC的平分线与AD交于点E,∴∠1=∠2,∠3=∠4,∴∠BED=∠1+∠3,∠DBE=∠4+∠CBD,∵∠CBD=∠2,∴∠BED=∠DBE,∴BD=DE.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
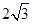 ,∠DPA=45°.
,∠DPA=45°.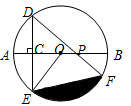
 ;
; ,∴AB=
,∴AB= ),C为直线AB上一点,过A、O、C的⊙E的半径为2.求线段OC的长.
),C为直线AB上一点,过A、O、C的⊙E的半径为2.求线段OC的长.
 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF, 设⊙O半径为x, EF为y.①y关于x的函数关系式;②求线段EF长度的最小值.
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF, 设⊙O半径为x, EF为y.①y关于x的函数关系式;②求线段EF长度的最小值.
 是
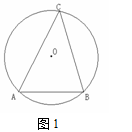
是 的内接三角形,
的内接三角形, ,
,  为
为 至点
至点 ,使
,使 .
.
 ;
; ,求证:
,求证: .
.


