题目内容
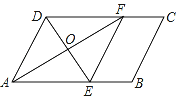
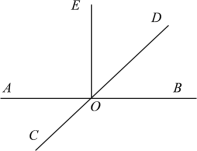
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
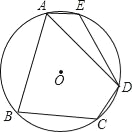
【答案】(1)∠AED=120°;(2)12.
【解析】试题分析:
(1)如图,连接BD,由已知条件证△ABD是等边三角形,得到∠ABD=60°,从而由圆内接四边形的性质可得∠AED=120°;
(2)如图,连接OA,由∠ABD=60°,可得∠AOD=120°,结合∠DOE=90°,可得∠AOE=30°,从而可得![]() .
.
试题解析:
(1)如图,连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴![]() .
.

【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如下图所示:

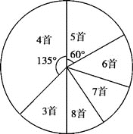
大赛结束后一个月,再次调查这部分学生“一周诗词诵背数量”,绘制成统计表:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人 数 | 10 | 10 | 15 | m | 25 | 20 |
请根据调查的信息
(1)本次调查抽取了多少名学生?
(2)补全条形统计图,在扇形统计图中,“6首”的圆心角为 度;
(3)表格中m的值为 ;
(4)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;