题目内容
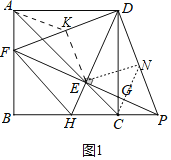
【题目】如图,正方形ABCD中,点H是边BC上一点(不与点B、点C重合).连接DH交正方形对角线AC于点E,过点E作DH的垂线交线段AB、CD于点F、G.延长FG与BC的延长线交于点P,连接DF、DP、FH.
(1)∠FDH=______°;DF与DP的位置关系是______,DF与DP的大小关系是______;
(2)在(1)的结论下,若AD=4,求△BFH的周长;
(3)在(1)的结论下,若BP=8,求AE的长.
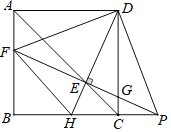
【答案】(1)45,DF⊥DP,DF=DP;(2)△BFH的周长= 8;(3)AE=4![]() .
.
【解析】
(1)取DF的中点K,连接AK,EK.想办法证明A,F,E,D四点共圆,推出∠DFE=∠DAE=45°,取PD中点N,连接EN,NC,同法可证:NE=NC=NP=ND,推出D,E,C,P四点共圆,推出∠DPE=∠DCE=45°,可得∠PDF=90°,△DFP是等腰直角三角形,即可解决问题;
(2)只要证明Rt△DAF≌Rt△DCF(HL),推出AF=CP,再证明FH=PH,即可推出△BFH的周长=BF+BH+FH=BF+BH+HP=BF+BH+CH+CP=BF+BC+AF=BC+AB=2AB=2AD;
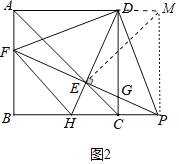
(3)如图2中,作EM⊥AE交AD的延长线于M,连接PM.想办法证明BP=AM,AM=![]() AE即可解决问题;
AE即可解决问题;
解:(1)取DF的中点K,连接AK,EK.
∵DH⊥FP,
∴∠DEF=90°,
∵四边形ABCD是正方形,
∴∠DAF=∠BCD=∠DCP=90°,∠DAC=∠DCA=45°,
∵FK=KD,
∴KA=KF=KD=KE,
∴A,F,E,D四点共圆,
∴∠DFE=∠DAE=45°,
取PD中点N,连接EN,NC,同法可证:NE=NC=NP=ND,
∴D,E,C,P四点共圆,
∴∠DPE=∠DCE=45°,
∴∠PDF=90°,△DFP是等腰直角三角形,
∴DF=DP,DF⊥DP,
∵DE⊥PF,
∴∠FDE=∠PDE=![]() ∠PDF=45°,
∠PDF=45°,
故答案为45,DF⊥DP,DF=DP.
(2)∵AD=DC,DF=DP,∠DAF=∠DCP=90°,
∴Rt△DAF≌Rt△DCF(HL),
∴AF=CP
∵DF=DP,DE⊥PF,
∴EF=PE,
∴FH=PH,
∴△BFH的周长=BF+BH+FH=BF+BH+HP=BF+BH+CH+CP=BF+BC+AF=BC+AB=2AB=2AD=8.
(3)如图2中,作EM⊥AE交AD的延长线于M,连接PM.
∵△DFE,△AEM都是等腰直角三角形,
∴EF=ED,EA=EM,
∵∠AEM=∠FED=90°,
∴∠AEF=∠DEM,
∴△AEF≌△MED(SAS),
∴AF=DM,
∵AF=PC,
∴DM=PC,
∵DM∥PC,∠DCP=90°,
∴四边形DCPM是矩形,四边形ABPM是矩形,
∴AM=BP,
∵AM=![]() AE,
AE,
∴BP=![]() AE,
AE,
∵PB=8,
∴AE=4![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】下表是小明某一周的收支情况,规定收入为正,支出为负.(单位:元)
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
15 | 12 | 0 | 20 | 15 | 10 | 14 |
8 | 12 | 19 | 10 | 9 | 11 | 8 |
(1)小明哪天的收入小于支出?答:
(2)小明这一周的平均支出是多少?
(3)小明这一周共有多少节余?