题目内容
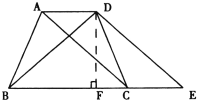
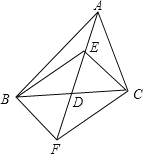
【题目】在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE = BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
【答案】见解析
【解析】
(1)由已知条件易得∠CED=∠BFD,BD=CD,结合∠BDF=∠CDE即可证得:△BDF≌△CDE;
(2)由△BDF≌△CDE易得DE=DF,结合BD=CD可得四边形BFCE是平行四边形,结合DE= BC可得EF=BC,由此即可证得平行四边形BFCE是矩形.
BC可得EF=BC,由此即可证得平行四边形BFCE是矩形.
(1)∵CE∥BF,
∴∠CED=∠BFD.
∵D是BC边的中点,
∴BD=DC,
在△BDF和△CDE中, ,
,
∴△BDF≌△CDE(AAS).
(2)四边形BFCE是矩形.理由如下:
∵△BDF≌△CDE,
∴DE=DF,
又∵BD=DC,
∴四边形BFCE是平行四边形.
∵DE= BC,DE=
BC,DE= EF,
EF,
∴BC=EF,
∴平行四边形BFCE是矩形.

练习册系列答案
相关题目