题目内容
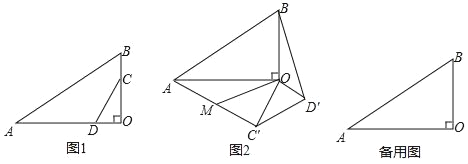
【题目】如图①,在平面直角坐标系中,抛物线y=ax2+bx+4![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点D,且3OC=4OB,对称轴为直线x=
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点D,且3OC=4OB,对称轴为直线x=![]() ,点E
,点E![]() ,连接CE交对称轴于点F,连接AF交抛物线于点G.
,连接CE交对称轴于点F,连接AF交抛物线于点G.
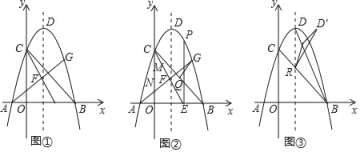
(1)求抛物线的解析式和直线CE的解析式;
(2)如图②,过E作EP⊥x轴交抛物线于点P,点Q是线段BC上一动点,当QG+![]() QB最小时,线段MN在线段CE上移动,点M在点N上方,且MN=
QB最小时,线段MN在线段CE上移动,点M在点N上方,且MN=![]() ,请求出四边形PQMN周长最小时点N的横坐标;
,请求出四边形PQMN周长最小时点N的横坐标;
(3)如图③,BC与对称轴交于点R,连接BD,点S是线段BD上一动点,将△DRS沿直线RS折叠至△D′RS,是否存在点S使得△D′RS与△BRS重叠部分的图形是直角三角形?若存在,请求出BS的长,若不存在,请说明理由.(参考数据:tan∠DBC=![]() )
)
【答案】(1)y=﹣2x+4![]() .(2)
.(2)![]() ;(3)BS的值为
;(3)BS的值为![]() 或
或![]() .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)如图1中,作QH⊥AB于H.首先求出直线AF的解析式,利用方程组求出点G坐标,再证明GQ+![]() BQ=GQ+QH,推出当G、Q、H三点共线时,GQ+
BQ=GQ+QH,推出当G、Q、H三点共线时,GQ+![]() BQ的值最小,最小值为
BQ的值最小,最小值为![]() ,此时Q(
,此时Q(![]() ,
,![]() ).如图2中,将点Q沿CE方向平移
).如图2中,将点Q沿CE方向平移![]() 个单位得到Q′,作点Q′关于直线CE的对称点Q″,连接PQ″交直线CE于M,此时四边形PQNM的周长最小.想办法求出点M的坐标即可解决问题;
个单位得到Q′,作点Q′关于直线CE的对称点Q″,连接PQ″交直线CE于M,此时四边形PQNM的周长最小.想办法求出点M的坐标即可解决问题;
(3)分两种情形,①如图3中,当RS⊥BD时,△D′RS与△BRS重叠部分的图形是直角三角形.②如图4中,当RD′⊥BD时,分别求解即可;
解:(1)由题意C(0,4![]() ),
),
∴OC=![]() ,
,
∵3OC=4OB,
∴OB=3![]() ,
,
∴B(3![]() ,0),
,0),
∵抛物线的对称轴x=![]() ,
,
∴A(﹣![]() ,0),
,0),
设抛物线的解析式为y=a(x+![]() )(x﹣3
)(x﹣3![]() ),把C(0,4
),把C(0,4![]() )代入得到a=﹣
)代入得到a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() (x2﹣2
(x2﹣2![]() x﹣9),即y=﹣
x﹣9),即y=﹣![]() +
+![]() x+4
x+4![]() .
.
设直线CE的解析式为y=kx+b,则有![]() ,解得
,解得![]() ,
,
∴直线CE的解析式为y=﹣2x+4![]() .
.
(2)如图1中,作QH⊥AB于H.

由(1)可知F(![]() ,2
,2![]() ),
),
∴直线AF的解析式为y=x+![]() ,
,
由 ,解得
,解得![]() 或
或 ,
,
∴G(![]() ,
,![]() ),
),
∵QH∥CO,BC=![]() =5
=5![]() ,
,
∴![]() ,
,
∴QH=![]() BQ,
BQ,
∴GQ+![]() BQ=GQ+QH,
BQ=GQ+QH,
∴当G、Q、H三点共线时,GQ+![]() BQ的值最小,最小值为
BQ的值最小,最小值为![]() ,此时Q(
,此时Q(![]() ,
,![]() ).
).
如图2中,将点Q沿CE方向平移![]() 个单位得到Q′,作点Q′关于直线CE的对称点Q″,连接PQ″交直线CE于M,此时四边形PQNM的周长最小.
个单位得到Q′,作点Q′关于直线CE的对称点Q″,连接PQ″交直线CE于M,此时四边形PQNM的周长最小.
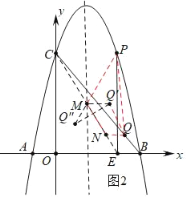
易知Q′(![]() ,2
,2![]() ),Q″(
),Q″(![]() ,
,![]() ),
),
∵P(2![]() ,4
,4![]() ),
),
∴直线PQ″的解析式为y=![]() x+
x+![]() ,
,
由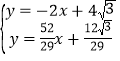 ,解得
,解得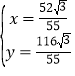 ,
,
∴M(![]() ,
,![]() ),
),
∵MN=![]() ,可得N(
,可得N(![]() ,
,![]() ),
),
∴点N的横坐标为![]() .
.
(3)如图3中,①当RS⊥BD时,△D′RS与△BRS重叠部分的图形是直角三角形.
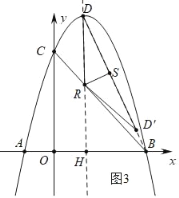
设抛物线的对称轴交x轴于H设抛物线的对称轴交x轴于H.由题意:BH=2![]() ,DH=
,DH=![]() ,BD=
,BD=![]() =
=![]()
![]() ,
,
∵RH∥CO,
∴![]() ,
,
∴RH=![]() ,DR=DH﹣RH=
,DR=DH﹣RH=![]() ,
,
∵△DRS∽△DBH,
∴![]() ,
,
∴RS=![]() ,DS=
,DS=![]() ,
,
∴BS=BD﹣DS=![]() .
.
②如图4中,当RD′⊥BD时,设垂足为K,作SG⊥DH于G.

∵∠SRD=∠SRD′,SG⊥RD,SK⊥RD′,
∴SG=SK,设SG=SK=n,
∵D(![]() ,
,![]() ),DR=RH=
),DR=RH=![]() ,BD=
,BD=![]() =
=![]() ,
,
在Rt△GSD中,∵DG2+SG2=SD2,
∴(![]() ﹣
﹣![]() )2+m2=(
)2+m2=(![]() ﹣m)2,
﹣m)2,
解得m=![]() ﹣
﹣![]() ,
,
∴SB=SK+BK=![]() ﹣
﹣![]() +
+![]() =
=![]() +
+![]()
综上所述,满足条件的BS的值为![]() 或
或![]() +
+![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案