题目内容
【题目】如图，利用一面长18米的墙，用篱笆围成一个矩形场地ABCD，设AD长为x米，AB长为y米，矩形的面积为S平方米．
(1)若篱笆的长为32米，求y与x的函数关系式，并直接写出自变量x的取值范围；
(2)在(1)的条件下，求S与x的函数关系式，并求出使矩形场地的面积为120平方米的围法．
【答案】(1)y=-2x+32(
)；(2)当AB长为12米，AD长为10米时，矩形的面积为120平方米.
【解析】
(1)根据2x+y=32，整理可得y与x的关系式，再结合墙长即可求得x的取值范围；
(2)根据长方形的面积公式可得S与x的关系式，再令S=120，可得关于x的方程，解方程即可求得答案.
(1)由题意2x+y=32，
所以y=-2x+32，
又
，解得7≤x<16，
所以y=-2x+32()；
(2)
，
，
∵
，
∴
，
，
(不合题意，舍去) ，
，
答：当AB长为12米，AD长为10米时，矩形的面积为120平方米.
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
【题目】学校为了提高学生跳远科目的成绩，对全校500名九年级学生开展了为期一个月的跳远科目强化训练．王老师为了了解学生的训练情况，强化训练前，随机抽取了该年级部分学生进行跳远测试，经过一个月的强化训练后，再次测得这部分学生的成绩，将两次测得的成绩制作成如图所示的统计图和不完整的统计表
训练后学生成绩统计表
成绩/分数 | 6分 | 7分 | 8分 | 9分 | 10分 |
人数/人 | 1 | 3 | 8 | 5 | n |
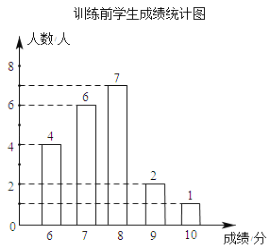
根据以上信息回答下列问题
（1）训练后学生成绩统计表中n= ，并补充完成下表：
平均分 | 中位数 | 众数 | |
训练前 | 7.5 | 8 | |
训练后 | 8 |
（2）若跳远成绩9分及以上为优秀，估计该校九年级学生训练后比训练前达到优秀的人数增加了多少？
