题目内容
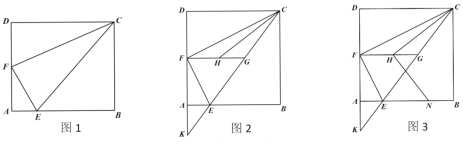
【题目】如图,四边形ABCD是正方形,点E是BC边上的点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)如图①,当点E是BC边上任一点(不与点B、C重合)时,求证:AE=EF.
(2)如图②当点E是BC边的延长线上一点时,(1)中的结论还成立吗? (填成立或者不成立).
(3)当点E是BC边上任一点(不与点B、C重合)时,若已知AE=EF,那么∠AEF的度数是否发生变化?证明你的结论.

【答案】(1)见解析;(2)成立,理由见解析;(3)∠AEF=90°不发生变化.理由见解析.
【解析】
(1)在AB上取点G,使得BG=BE,连接EG,根据已知条件利用ASA判定△AGE≌△ECF,因为全等三角形的对应边相等,所以AE=EF;
(2)在BA的延长线上取一点G,使AG=CE,连接EG,根据已知利用ASA判定△AGE≌△ECF,因为全等三角形的对应边相等,所以AE=EF;
(3)在BA边取一点G,使BG=BE,连接EG.作AP⊥EG,EQ⊥FC,先证AGP≌△ECQ得AP=EQ,再证Rt△AEP≌Rt△EFQ得∠AEP=∠EFQ,∠BAE=∠CEF,结合∠AEB+∠BAE=90°知∠AEB+∠CEF=90°,从而得出答案.
(1)证明:在BA边取一点G,使BG=BE,连接EG,
∵四边形ABCD是正方形,
∴∠B=90°,BA=BC,∠DCM═90°,
∴BA-BG=BC-BE,
即AG=CE.
∵∠AEF=90°,∠B=90°,
∴∠AEB+∠CEF=90°,∠AEB+∠BAE=90°,
∴∠CEF=∠BAE.
∵BG=BE,CF平分∠DCM,
∴∠BGE=∠FCM=45°,
∴∠AGE=∠ECF=135°,
∴△AGE≌△ECF(ASA),
∴AE=EF.
(2)成立,
理由:在BA的延长线上取点G,使得AG=CE,连接EG.
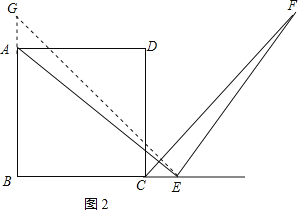
∵四边形ABCD为正方形,AG=CE,
∴∠B=90°,BG=BE,
∴△BEG为等腰直角三角形,
∴∠G=45°,
又∵CF为正方形的外角平分线,
∴∠ECF=45°,
∴∠G=∠ECF=45°,
∵∠AEF=90°,
∴∠FEM=90°-∠AEB,
又∵∠BAE=90°-∠AEB,
∴∠FEM=∠BAE,
∴∠GAE=∠CEF,
在△AGE和△ECF中,
∵ ,
,
∴△AGE≌△ECF(ASA),
∴AE=EF.
故答案为:成立.
(3)∠AEF=90°不发生变化.
理由如下:在BA边取一点G,使BG=BE,连接EG.分别过点A、E作AP⊥EG,EQ⊥FC,垂足分别为点P、Q,
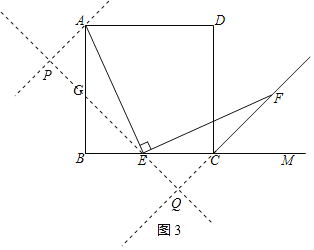
∴∠APG=∠EQC=90°,
由(1)中知,AG=CE,∠AGE=∠ECF=135°,
∴∠AGP=∠ECQ=45°,
∴△AGP≌△ECQ(AAS),
∴AP=EQ,
∴Rt△AEP≌Rt△EFQ(HL),
∴∠AEP=∠EFQ,
∴∠BAE=∠CEF,
又∵∠AEB+∠BAE=90°,
∴∠AEB+∠CEF=90°,
∴∠AEF=90°.

【题目】学校为了提高学生跳远科目的成绩,对全校500名九年级学生开展了为期一个月的跳远科目强化训练.王老师为了了解学生的训练情况,强化训练前,随机抽取了该年级部分学生进行跳远测试,经过一个月的强化训练后,再次测得这部分学生的成绩,将两次测得的成绩制作成如图所示的统计图和不完整的统计表
训练后学生成绩统计表
成绩/分数 | 6分 | 7分 | 8分 | 9分 | 10分 |
人数/人 | 1 | 3 | 8 | 5 | n |
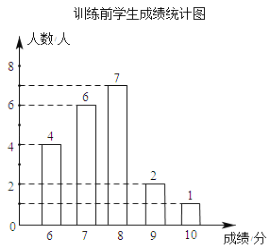
根据以上信息回答下列问题
(1)训练后学生成绩统计表中n= ,并补充完成下表:
平均分 | 中位数 | 众数 | |
训练前 | 7.5 | 8 | |
训练后 | 8 |
(2)若跳远成绩9分及以上为优秀,估计该校九年级学生训练后比训练前达到优秀的人数增加了多少?