题目内容
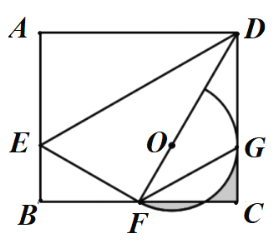
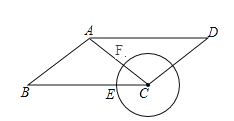
【题目】如图,平行四边形ABCD中,AB=5,BC=8,cosB=![]() ,点E是BC边上的动点,以C为圆心,CE长为半径作圆C,交AC于F,连接AE,EF.
,点E是BC边上的动点,以C为圆心,CE长为半径作圆C,交AC于F,连接AE,EF.
(1)求AC的长;
(2)当AE与圆C相切时,求弦EF的长;
(3)圆C与线段AD没有公共点时,确定半径CE的取值范围.
【答案】(1)AC=5;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)过A作AG⊥BC于点G,由![]() ,得到BG=4,AG=3,然后由勾股定理即可求出AC的长度;
,得到BG=4,AG=3,然后由勾股定理即可求出AC的长度;
(2)当点E与点G重合时,AE与圆C相切,过点F作FH⊥CE,则CE=CF=4,则CH=3.2,FH=2.4,得到EH=0.8,由勾股定理,即可得到EF的长度;
(3)根据题意,可分情况进行讨论:①当圆C与AD相离时;②当CE>CA时;分别求出CE的取值范围,即可得到答案.
解:(1)过A作AG⊥BC于点G,如图:

在Rt△ABG中,AB=5,![]() ,
,
∴BG=4,
∴AG=3,
∴![]() ,
,
∴点G是BC的中点,
在Rt△ACG中,![]() ;
;
(2)当点E与点G重合时,AE与圆C相切,过点F作FH⊥CE,如图:

∴CE=CF=4,
∵AB=AC=5,
∴∠B=∠ACB,
∴![]() ,
,
∴CH=3.2,
在Rt△CFH中,由勾股定理,得
FH=2.4,
∴EH=0.8,
在Rt△EFH中,由勾股定理,得
![]() ;
;
(3)根据题意,圆C与线段AD没有公共点时,可分为以下两种情况:
①当圆C与AD相离时,则CE<AE,

∴半径CE的取值范围是:![]() ;
;
②当CE>CA时,点E在线段BC上,
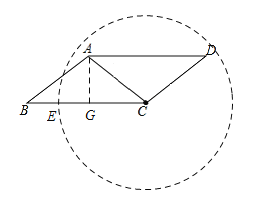
∴半径CE的取值范围是:![]() ;
;
综合上述,半径CE的取值范围是:![]() 或
或![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】在世界环境日(6月5日),学校组织了保护环境知识测试,现从中随机抽取部分学生的成绩作为样本,按“优秀”“良好”“合格”“不合格”四个等级进行统计,绘制了如下尚不完整的统计图表.
测试成绩统计表
等级 | 频数(人数) | 频率 |
优秀 | 30 |
|
良好 |
| 0.45 |
合格 | 24 | 0.20 |
不合格 | 12 | 0.10 |
合计 |
| 1 |

根据统计图表提供的信息,解答下列问题:
(1)表中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)补全条形统计图;
(3)若该校有2400名学生参加了本次测试,估计测试成绩等级在良好以上(包括良好)的学生约有多少人?