题目内容
【题目】二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() 秒.
秒.
(1)求二次函数![]() 的表达式:
的表达式:
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积:
的面积:
(3)在直线![]() 上存在一点
上存在一点![]() ,当
,当![]() 是以
是以![]() 为直角的等腰直角三角形时,求此时点
为直角的等腰直角三角形时,求此时点![]() 的坐标;
的坐标;
(4)当![]() 时,在直线
时,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标
的坐标
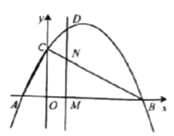
【答案】(1)![]() (2)2(3)
(2)2(3)![]() (4)
(4)![]() 或
或![]()
【解析】
(1)直接将A、B两点的坐标代入列方程组解出即可;
(2)根据题意得出AM,OM,设![]() 的解析式为:
的解析式为:![]() ,将点
,将点![]() 代入求出解析式,然后将
代入求出解析式,然后将![]() 分别代入
分别代入![]() 和
和![]() 中,得:
中,得:![]() ,再根据三角形面积公式,即可解答
,再根据三角形面积公式,即可解答
(3)过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() ,根据题意得出
,根据题意得出![]() ,根据
,根据![]() ,即可解答
,即可解答
(4)当![]() 时,
时,![]() ,此时
,此时![]() 点在二次函数的对称轴上,以
点在二次函数的对称轴上,以![]() 点为圆心,
点为圆心,![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() 两点,得出
两点,得出![]() ,再根据
,再根据![]() (同弧所对圆周角),即可解答
(同弧所对圆周角),即可解答
(1)将点![]() 代入
代入![]() ,得:
,得:
![]()
解得: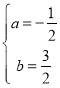
所以,二次函数的表达方式为:![]()
(2)![]()
又![]()
设![]() 的解析式为:
的解析式为:![]() ,将点
,将点![]() 代入,得:
代入,得:
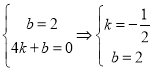
所以,直线![]() 的解析式为:
的解析式为:![]() .
.
将![]() 分别代入
分别代入![]() 和
和![]() 中,得:
中,得:![]() .
.
![]()
![]() .
.
(3)假设过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 的延长线于点
的延长线于点![]() ,
,
设![]() ,由题意得:
,由题意得:
![]()
![]()
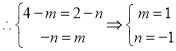
所以,点![]() 的坐标为:
的坐标为:![]()
(4)当![]() 时,
时,![]() ,此时
,此时![]() 点在二次函数的对称轴上,
点在二次函数的对称轴上,
以![]() 点为圆心,
点为圆心,![]() 长为半径作圆,交
长为半径作圆,交![]() 于
于![]() 两点
两点
![]()
![]()
![]() 点在该圆上
点在该圆上
![]()
![]()
![]() (同弧所对圆周角)
(同弧所对圆周角)
![]()
![]()
![]() 或
或![]()

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目