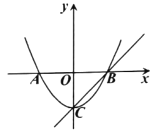
题目内容
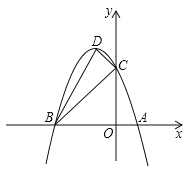
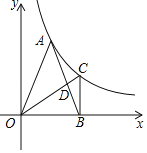
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求二次函数![]() 的解析式;
的解析式;
(3)作直线![]() ,问抛物线
,问抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .若存在,求出点
.若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)点B的坐标为(6,0);(2)二次函数的解析式为![]() ;(3)点M的坐标为
;(3)点M的坐标为![]() 或
或![]()
【解析】
(1)由条件可知OC=6,根据OB=OC,可求出点B的坐标;
(2)将B,C两点的坐标代入y=ax2+b,求出a,b的值,即可求得二次函数的解析式;
(3)根据题意,分M在BC上方和下方两种情况进行解答,画出相应的图形,然后根据二次函数的性质和锐角三角函数可以求得点M的坐标.
解:(1)∵C(0,-6)
∴![]()
∵![]()
∴![]()
∴点B的坐标为(6,0)
(2)∵抛物线![]() (
(![]() ≠0)经过点C(0,-6)和点B(6,0),
≠0)经过点C(0,-6)和点B(6,0),
∴![]() ,解得
,解得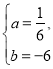
∴该二次函数的解析式为![]()
(3)存在
①若点M在BC上方,设MC交![]() 轴于点D,则∠ODC=45°+15°=60°.
轴于点D,则∠ODC=45°+15°=60°.
∴∠OCD=30°.
∴设OD=![]() ,则CD=2
,则CD=2![]() .
.
∵在Rt△OCD中,∠COD=90°,OC=6,
∴![]() ,
,
即![]() ,
,
解得![]() (舍),
(舍),![]() .
.
∴点D的坐标为(![]() ,0).
,0).
设直线DC的函数解析式为![]()
∴![]() ,解得
,解得![]()
∴直线DC的函数解析式为![]()
∴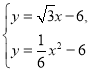 ,解得
,解得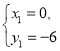 (舍),
(舍),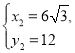
∴![]() (
(![]() ,12)
,12)
②若点M在BC下方,设MC交![]() 轴于点E,则∠OEC=45°-15°=30°.
轴于点E,则∠OEC=45°-15°=30°.
∵OC=6,则CE=12.
∵在Rt△OCE中,∠COE=90°,
∴![]() =108,∴
=108,∴![]() .
.
∴点E的坐标为(![]() ,0).
,0).
设直线EC的函数解析式为![]() ,
,
∴![]() ,解得
,解得![]()
∴直线EC的函数解析式为![]()
∴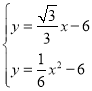 ,解得
,解得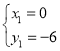 (舍),
(舍),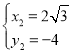 .
.
∴![]()
综上所述,点M的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目