ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΘ®Ε· ÷≤ΌΉςΘ©
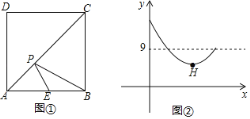
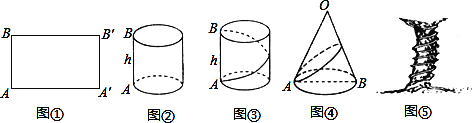
»γΆΦΔΌΘ§Α―≥ΛΈΣlΓΔΩμΈΣhΒΡΨΊ–ΈΨμ≥…“‘ABΈΣΗΏΒΡ‘≤÷υ–ΈΘ§‘ρΒψAΓδ”κΒψ______÷ΊΚœΘ§ΒψBΓδ”κΒψ______÷ΊΚœΘΜ
Θ®ΧΫΨΩΖΔœ÷Θ©
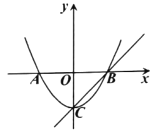
»γΆΦΔΎΘ§‘≤÷υΒΡΒΉΟφ÷ή≥Λ «80Θ§ΗΏ «60Θ§»τ‘Ύ‘≤÷υΧεΒΡ≤ύΟφ»Τ“Μ»ΠΥΩœΏΉςΉΑ ΈΘ§¥”œ¬ΒΉΟφA≥ωΖΔΘ§―Ί‘≤÷υ≤ύΟφ»Τ“Μ÷ήΒΫ…œΒΉΟφBΘ§‘ρ’βΧθΥΩœΏΉνΕΧΒΡ≥ΛΕ» «______ΘΜ
Θ® ΒΦυ”Π”ΟΘ©
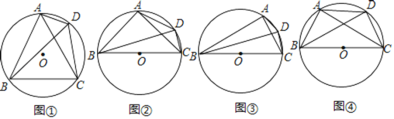
»γΆΦΔέΘ§‘≤ΉΕΒΡΡΗœΏ≥ΛΈΣ12Θ§ΒΉΟφΑκΨΕΈΣ4Θ§»τ‘Ύ‘≤ΉΕΧεΒΡ≤ύΟφ»Τ“Μ»Π≤ ¥χΉωΉΑ ΈΘ§¥”‘≤ΉΕΒΡΒΉΟφ…œΒΡΒψA≥ωΖΔΘ§―Ί‘≤ΉΕ≤ύΟφ»Τ“Μ÷ήΜΊΒΫΒψAΘ°«σ’βΧθ≤ ¥χΉνΕΧΒΡ≥ΛΕ» «Εύ…ΌΘΩ
Θ®ΆΊ’ΙΝΣœκΘ©
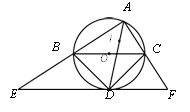
»γΆΦΔήΘ§“ΜΩ≈Ι≈ ς…œœ¬¥÷œΗœύ≤ν≤Μ¥σΘ§Ω…“‘Ω¥≥…‘≤÷υΧεΘ°≤βΒΟ ςΗ…ΒΡ÷ή≥ΛΈΣ3ΟΉΘ§ΗΏΈΣ18ΟΉΘ§”–“ΜΗυΉœΧΌΉ‘ ςΒΉ≤ΩΨυ‘»ΒΡ≈Χ»Τ‘Ύ ςΗ……œΘ§«ΓΚΟ»Τ8÷ήΒΫ¥ο ςΗ…ΒΡΕΞ≤ΩΘ§’βΧθΉœΧΌ÷Ν…Ό”– ΟΉ
ΓΨ¥πΑΗΓΩΓΨΕ· ÷≤ΌΉςΓΩΘΚAΘ§BΘΜΓΨΧΫΨΩΖΔœ÷ΓΩ100 ΘΜΓΨ ΒΦυ”Π”ΟΓΩΘΚ![]() ΘΜΓΨΆΊ’ΙΝΣœκΓΩ30
ΘΜΓΨΆΊ’ΙΝΣœκΓΩ30
ΓΨΫβΈωΓΩ
[Ε· ÷≤ΌΉς]ΗυΨί‘≤÷υΒΡ≤ύΟφ’ΙΩΣΆΦ «ΨΊ–ΈΦ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
[ΧΫΨΩΖΔœ÷] Ν§Ϋ”![]() Θ§ΗυΨίΨΊ–ΈΒΡ–‘÷ ΦΑΙ¥Ι…Ε®άμ«σ≥ω
Θ§ΗυΨίΨΊ–ΈΒΡ–‘÷ ΦΑΙ¥Ι…Ε®άμ«σ≥ω![]() Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
[ ΒΦυ”Π”Ο]ΫΪ‘≤ΉΕ’ΙΩΣΒΟΒΫ’ΙΩΣΆΦΘ§Ν§Ϋ”![]() Θ§ΗυΨίΜΓ≥ΛΙΪ Ϋ«σ≥ωΓœ
Θ§ΗυΨίΜΓ≥ΛΙΪ Ϋ«σ≥ωΓœ![]() ΒΡΕ» ΐΘ§ΙΐΒψOΉςODΓΆ
ΒΡΕ» ΐΘ§ΙΐΒψOΉςODΓΆ![]() ”ΎΒψDΘ§ΗυΨίΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΦΑ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ «σ≥ωOD=6Θ§‘Όάϊ”ΟΙ¥Ι…Ε®άμ«σ≥ωADΦ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
”ΎΒψDΘ§ΗυΨίΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΦΑ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ «σ≥ωOD=6Θ§‘Όάϊ”ΟΙ¥Ι…Ε®άμ«σ≥ωADΦ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
[ΆΊ’ΙΝΣœκ]ΫΪ ςΗ…ΒΡΗΏΕ»Ζ÷≥…œύΒ»ΒΡ8ΕΈΘ§άϊ”Ο ςΗ…ΒΡ÷ή≥ΛΫ®ΝΔΙ¥Ι…Ε®άμΒΡΒ» Ϋ«σ≥ω“Μ»ΠΉœΧΌΒΡ≥ΛΘ§”…¥ΥΒΟΒΫ¥πΑΗ.
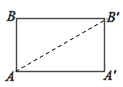
[Ε· ÷≤ΌΉς]Βψ![]() ”κΒψA÷ΊΚœΘ§Βψ
”κΒψA÷ΊΚœΘ§Βψ![]() ”κΒψB÷ΊΚœΘ§
”κΒψB÷ΊΚœΘ§
Ι ¥πΑΗΈΣΘΚAΘ§BΘΜ
[ΧΫΨΩΖΔœ÷]”…Χβ“β÷ΣΗΟ‘≤÷υΒΡ≤ύΟφ’ΙΩΣΆΦΦ¥ «ΨΊ–Έ![]() Θ§‘ρ
Θ§‘ρ![]() =80Θ§
=80Θ§![]() =60Θ§
=60Θ§
Ν§Ϋ”![]() Θ§
Θ§
ΓΏΓœ![]() =90ΓψΘ§
=90ΓψΘ§
Γύ![]() ,
,
Γύ’βΧθΥΩœΏΉνΕΧΒΡ≥ΛΕ» «100Θ§
Ι ¥πΑΗΈΣΘΚ100ΘΜ
[ ΒΦυ”Π”Ο]
ΫβΘΚ‘≤ΉΕΒΡ≤ύΟφ’ΙΩΣΆΦΘ§»γΆΦΥυ ΨΘΚ
Ν§Ϋ”![]() Θ§
Θ§
‘ρ![]() ΈΣΉνΕΧ¬ΖΨΕΘ°
ΈΣΉνΕΧ¬ΖΨΕΘ°
ΜΓ![]() ΒΡ≥ΛΈΣΘΚ
ΒΡ≥ΛΈΣΘΚ![]() Θ§
Θ§
”…ΜΓ≥ΛΙΪ ΫΒΟΓœ![]() ΒΡΕ» ΐΈΣΘΚ
ΒΡΕ» ΐΈΣΘΚ![]()
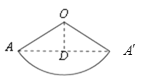
ΙΐΒψOΉςODΓΆ![]() ”ΎΒψDΘ§
”ΎΒψDΘ§
ΓύΓœAOD=60ΓψΘ§
ΓύΓœOAD=30ΓψΘ§
ΓύOD=6Θ§
‘ΎRtΓςAOD÷–![]() Θ§
Θ§
Γύ’βΧθ≤ ¥χΉνΕΧΒΡ≥ΛΕ» «![]() ΘΜ
ΘΜ
[ΆΊ’ΙΝΣœκ]ΓΏ ςΗ…ΒΡΗΏ «18ΟΉΘ§≤χ»Τ8»ΠΉœΧΌΘ§
ΓύΟΩœύΝΎΝΫ»ΠΉœΧΌΒΡΨύάκ «![]() ΟΉΘ§
ΟΉΘ§
ΓΏ ςΗ…ΒΡ÷ή≥Λ «3ΟΉΘ§
Γύ“Μ»ΠΉœΧΌΒΡ≥ΛΕ» «![]() ΟΉΘ§
ΟΉΘ§
Γύ8»ΠΉœΧΌΒΡ≥ΛΕ»Ήν…Ό «![]() ΟΉΘ§
ΟΉΘ§
Ι ¥πΑΗΈΣΘΚ30.

 ΩΣ–ΡΝΖœΑΩΈΩΈΝΖ”κΒΞ‘ΣΦλ≤βœΒΝ–¥πΑΗ
ΩΣ–ΡΝΖœΑΩΈΩΈΝΖ”κΒΞ‘ΣΦλ≤βœΒΝ–¥πΑΗ