题目内容
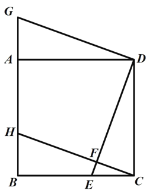
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

【答案】(1)证明见解析;(2)1.
【解析】试题分析:(1)这两个三角形中,已知的条件有∠DAE=∠EBF=90°,
那么只要得出另外一组对应角相等即可得出两三角形相似,因为∠ADE+∠DEA=90°.
而∠AED+∠FEB=90°,因此∠ADE=∠FEB.那么就构成了两三角形相似的条件;
(2)可用![]() 表示出BE的长,然后根据(1)中△ADE∽△BEF.可得出关于
表示出BE的长,然后根据(1)中△ADE∽△BEF.可得出关于![]() 的比例关系式,然后就能得出一个关于
的比例关系式,然后就能得出一个关于![]() 的函数关系式.根据函数的性质即可得出
的函数关系式.根据函数的性质即可得出![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
试题解析:(1) ![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
∴∠DAE=∠EBF=90°,
∴∠ADE+∠DEA=90°.
又EF⊥DE,
∴∠AED+∠FEB=90°,
∴∠ADE=∠FEB.
∴△ADE∽△BEF.
(2) 由(1)△ADE∽△BEF,AD=4,BE=4-x,得![]() ,得y=
,得y=![]() (-x2+4x)
(-x2+4x)
=![]() [-(x-2)2+4]=-
[-(x-2)2+4]=- ![]() (x-2)2+1,
(x-2)2+1,
∴当x=2时,y有最大值,y的最大值为1.

练习册系列答案
相关题目