题目内容
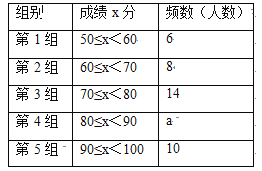
【题目】如图,四边形ABCD是平行四边形,OA=2,AB=6点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,点D在直线AO上,点F在x轴的正半轴上,则直线DE的表达式__________________.
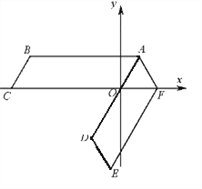
【答案】![]()
【解析】根据旋转的性质以及平行四边形的性质得出∠BAO=∠AOF=∠AFO=∠OAF,进而求出D、E点坐标,利用待定系数法求出直线DE的表达式.
解:如图所示:过点D作DM⊥x轴于点M,
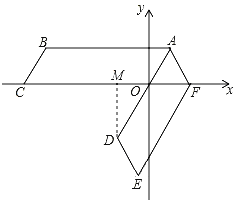
由题意可得:∠BAO=∠OAF,AO=AF,AB∥OC,
则∠BAO=∠AOF=∠AFO=∠OAF,
故∠AOF=60°=∠DOM,
∵OD=AD﹣OA=AB﹣OA=6﹣2=4,
∴MO=2,MD=2![]() ,
,
∴D(﹣2,﹣2![]() ),
),
过点E作EN⊥x轴于点N,
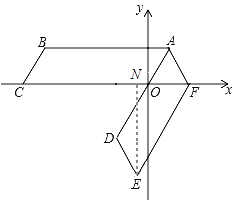
由题意可得: AD∥EF,∠AOF =60°
∴∠NFE=60°,∠NEF=30°,在Rt△ENF中,
FN=![]() EF=
EF=![]() ×6=3,
×6=3,
ON=FN﹣OF=3﹣2=1,
NE=![]() ,
,
∴E(﹣1,﹣![]() ),
),
设直线DE的表达式为y=kx+b,把D、E的坐标代入y=kx+b,得![]() .
.
“点睛”此题主要考查了平行四边形的性质以及求一次函数的解析式,正确得出D、E点坐标是解题关键.

练习册系列答案
相关题目