题目内容
【题目】阅读材料并解答问题：
关于勾股定理的研究有一个很重要的内容是勾股数组，在数学课本中我们已经了解到，“能够成为直角三角形三条边的三个正整数称为勾股数”，以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：
方法1：若m为奇数（m≥3），则a=m，b=
（m2﹣1）和c=
（m2+1）是勾股数．
方法2：若任取两个正整数m和n（m＞n），则a=m2﹣n2，b=2mn，c=m2+n2是勾股数．
（1）在以上两种方法中任选一种，证明以a，b，c为边长的△ABC是直角三角形；
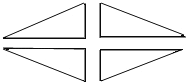
（2）某园林管理处要在一块绿地上植树，使之构成如下图所示的图案景观，该图案由四个全等的直角三角形组成，要求每个三角形顶点处都植一棵树，各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，且每个三角形的各边长之比为5：12：13，那么这四个直角三角形的边长共需植树 棵．
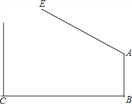
（3）某家俱市场现有大批如图所示的梯形边角余料(单位：cm)，实验初中数学兴趣小组决定将其加工成等腰三角形，且方案如下：
三角形中至少有一边长为10 cm；三角形中至少有一边上的高为8 cm，
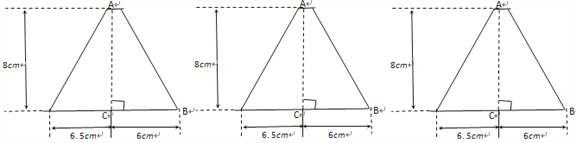
请设计出三种面积不同的方案并在图上画出分割线，求出相应图形面积.
【答案】（1）证明见解析；
（2）120；
（3）画分割线见解析，面积分别为48 cm
、40cm
和
cm
的等腰三角形.
【解析】试题分析：（1）先比较三边的大小，确定为斜边的是c，再求a2+b2=[
（m2+1）]2=c2；
（2）由各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，可得三角形最短边为5米，又有各边长之比为5：12：13，可得其他两边分别为12、13米．则每个三角形的边长可植树5+12+13=30棵，四个直角三角形的边长共需植树120棵．
（3）由图形可知，要求有又一边为10cm，可以将其作为三角形的一斜边，将另一边的边长截为10cm．利用勾股定理和三角形求面积公式，即可求出．
【解答】解：（1）方法1、c-a=
（m2+1）-m=
（m2-2m+1）=
（m-1）2＞0，c-b=1＞0，
所以c＞a，c＞b．而a2+b2=m2+[
（m2-1）]2=（
m4-2m2+1）+m2
=
（m4+2m2+1）=[
（m2+1）]2=c2，
所以以a、b、c为边的三角形是直角三角形．
（2）∵各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，
∴三角形最短边为5米，
又∵各边长之比为5：12：13，
∴其他两边分别为12、13米．
∴每个三角形的边长可植树5+12+13=30棵，
∴四个直角三角形的边长共需植树120棵．
（3）
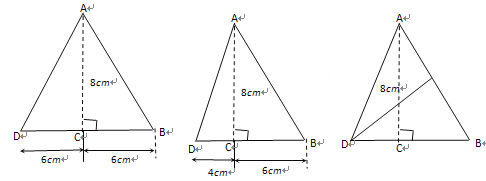
解：由勾股定理得：AB=
则
如图（1）AD=AB=10 cm时，BD=6 cm，S
=
=48 cm
；
如图（2）BD=AB=10 cm时，S
=
=40cm
如图（3）线段AB的垂直平分线交BC延长线于点D，则AB=10，设DC=x，则AD=BD=6+x,
在Rt△ACD中
，S
=
=
；
答：面积分别为48 cm
、40cm
和
cm
的等腰三角形
