题目内容
【题目】四边形的四边顺次为a、b、c、d,且满足a2+b2+c2+d2=2(ab+cd),则这个四边形一定是( )
A.平行四边形
B.两组对角分别相等的四边形
C.对角线互相垂直的四边形
D.对角线长相等的四边形
【答案】C
【解析】解:∵a2+b2+c2+d2=2ab+2cd, ∴a2+b2+c2+d2﹣2ab﹣2cd=0,
∴(a﹣b)2+(c﹣d)2=0,
∴a﹣b=0且c﹣d=0,
∴a=b且c=d.
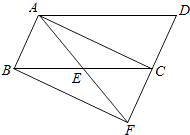
如图,点A在BD的垂直平分线上,点C在BD的垂直平分线上,
∴AC垂直平分线BD,
∴四边形ABCD是对角线互相垂直的四边形.
故选C.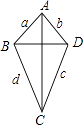
首先把a2+b2+c2+d2=2ab+2cd变形为a2+b2+c2+d2﹣2ab﹣2cd=0,然后利用完全平方公式分解因式和非负数的性质即可求解.

练习册系列答案
相关题目